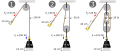Wright State University Lake Campus/2018-9/Phy1110/Notes

Page bottom

Mon 27 AugQB/a02 1Dkinem definitions

• QB/a02 1Dkinem definitions Class did all these questions in groups.

Wed 29 Aug Ohio State Coding

OSU coding videos Template:Cot

*airhead-straw-cleaner: start by creating canvas 500x500 centers it.
Then, tell computer to draw by  calling  "function draw(){
fill }"
*Learned how define variable, but truggling with found an "variables are not functions"
One of the laptops had no internet access, but nevertheless an account was made.
one account

Big Group
fill and text size.  Most seem to like it.  Redshirt felt they made progress, which is impressive b/c Redshirt didn't know how to code.

Conclusion:  This looks like a good project.

Wed 31 Aug 1D and 2D motion

QB/b_motionSimpleArithmetic and started QB/a03_2Dkinem_2dmotion

Wed 5 Sep Lab: Rolling ball (Excel)

trial 2
t(s)	x(cm)
0	0
1	36
2	70
3	109
4	157

We rolled a ping down a table that set and an angle 3.5/180 radian. starting at zero seconds, we measured the distance traveled. WE did the experiment three times and only one gave us a parabola.

A quick estimate of the epected acceralation was obtained by a best fit a parabola. We measured a=3.5 cm/s^2 but estimated a≈20cm/s^2.

The class learned how to convert these date into velocity versus time.

Fri 7 Sep Quizzes

{{#lst:Quizbank/College Physics Sem 1|1}}

Clueless about Mon but Wed 12 September ...

Half the class experimented and the other half conceptualized. All present on a half-finished lab.

14 September 2018 First effort by PHY1110 and 1050

All but the student supervisor were present, but we got by with a new boss. In HTW noRake (shovel) was absent.

• click image to expand
  click image to expand
• click image to expand
  click image to expand

x	y
0	0
21	10.8
32	24.5
39.5	40.2
46.5	65.5
54.2	98.1
55.5	123.7
57.7	147.3
57.7	179

12:59, 8 October 2018 (UTC)

Quizbank/College Physics Sem 1/T2

7/19 from Special:Permalink/1863392 to QB/b_velocityAcceleration
1/4 from Special:Permalink/1863116 to QB/a04DynForce Newton_forces
2/4 from Special:Permalink/1863117 to QB/a04DynForce Newton_sled
2/5 from Special:Permalink/1863118 to QB/a04DynForce Newton_tensions
1/5 from Special:Permalink/1863119 to QB/a05frictDragElast_3rdLaw
2/5 from Special:Permalink/1863120 to QB/a06uniformCircMotGravitation_friction

16:00, 10 October 2018 (UTC)

• 
• 
• 

For example

1. π can be ascertained using a circle and a ruler. But we can look for a way to do it on a spreadsheet.
2. e was discovered by Euler who was trying to model the explosion inside a cannon (or something like that...). But we can use a spreadsheet to "discover" using compound interest.
3. i is a tough one. It is most easily defined through i²=−1, but I think we need to also prove that (−1)² is not −1. That takes a little bit of geometry (easy to do).
4. Given all this, you can write an Excel spreadsheet to show that e^iπ≈−1 to very high precision.

Finding pi: https://www.youtube.com/watch?v=_rJdkhlWZVQ

Final_Project

Final Project: These problems are also available in OpenStax College Physics, which is licensed under a Creative Commons Attribution 4.0 License.

The project covers chapters 8-15

Linear Momentum and Collisions

Template:Hidden begin {{#lst:Physics_equations/Equations|08-Linear_Momentum_and_Collisions}}Template:Hidden end

EXAMPLE 8.7 DETERMINING THE FINAL VELOCITY OF AN UNSEEN OBJECT FROM THE SCATTERING OF ANOTHER OBJECT Suppose the following experiment is performed. A 0.250-kg object (m1) is slid on a frictionless surface into a dark room, where it strikes an initially stationary object with mass of 0.400 kg (m2). The 0.250-kg object emerges from the room at an angle of 45.0º with its incoming direction.

• Problem 47 A 3000-kg cannon is mounted so that it can recoil only in the horizontal direction. (a) Calculate its recoil velocity when it fires a 15.0-kg shell at 480 m/s at an angle of 20.0º above the horizontal. (b) What is the kinetic energy of the cannon? This energy is dissipated as heat transfer in shock absorbers that stop its recoil. (c) What happens to the vertical component of momentum that is imparted to the cannon when it is fired?

Statics and Torque

• delete templates above

{{#lst:Physics_equations/Equations|09-Statics_and_Torque}}Template:Hidden end

EXAMPLE 9.5 DO NOT LIFT WITH YOUR BACK Consider the person lifting a heavy box with his back, shown in Figure 9.30. (a) Calculate the magnitude of the force FB– in the back muscles that is needed to support the upper body plus the box and compare this with his weight. The mass of the upper body is 55.0 kg and the mass of the box is 30.0 kg. (b) Calculate the magnitude and direction of the force FV– exerted by the vertebrae on the spine at the indicated pivot point. Again, data in the figure may be taken to be accurate to three significant figures.

• Problem 14. A sandwich board advertising sign is constructed as shown in Figure 9.35 . The sign’s mass is 8.00 kg. (a) Calculate the tension in the chain assuming no friction between the legs and the sidewalk. (b) What force is exerted by each side on the hinge?
• Problem 15 refers to the previous question: (a) What minimum coefficient of friction is needed between the legs and the ground to keep the sign in Figure 9.35 in the position shown if the chain breaks? (b) What force is exerted by each side on the hinge?

Rotational Motion and Angular Momentum

Template:Hidden begin {{#lst:Physics_equations/Equations|10-Rotational_Motion_and_Angular Momentum}}Template:Hidden end

EXAMPLE 10.13 CALCULATING THE TORQUE IN A KICK The person whose leg is shown in Figure 10.22 kicks his leg by exerting a 2000-N force with his upper leg muscle. The effective perpendicular lever arm is 2.20 cm. Given the moment of inertia of the lower leg is 1.25 kg⋅m2, (a) find the angular acceleration of the leg. (b) Neglecting the gravitational force, what is the rotational kinetic energy of the leg after it has rotated through 57.3º (1.00 rad)?

• Problem 20. Unreasonable ResultsAn advertisement claims that an 800-kg car is aided by its 20.0-kg flywheel, which can accelerate the car from rest to a speed of 30.0 m/s. The flywheel is a disk with a 0.150-m radius. (a) Calculate the angular velocity the flywheel must have if 95.0% of its rotational energy is used to get the car up to speed. (b) What is unreasonable about the result? (c) Which premise is unreasonable or which premises are inconsistent?

Fluid Statics

Template:Hidden begin {{#lst:Physics_equations/Equations|11-Fluid_statics}}Template:Hidden end

EXAMPLE 11.10 CALCULATING DENSITY: IS THE COIN AUTHENTIC? The mass of an ancient Greek coin is determined in air to be 8.630 g. When the coin is submerged in water as shown in Figure 11.25, its apparent mass is 7.800 g. Calculate its density, given that water has a density of 1.000g/cm3 and that effects caused by the wire suspending the coin are negligible.

• Problem 39. If your body has a density of 995 kg/m3, what fraction of you will be submerged when floating gently in: (a) freshwater? (b) salt water, which has a density of 1027 kg/m3?

Fluid Dynamics

Template:Hidden begin {{#lst:Physics_equations/Equations|12-Fluid_dynamics}}Template:Hidden end

Temperature, Kinetic Theory, and Gas Laws

Template:Hidden begin {{#lst:Physics_equations/Equations|13-Temperature,_Kinetic Theory,_and_Gas_Laws}}Template:Hidden end

EXAMPLE 13.3 CALCULATING LINEAR THERMAL EXPANSION: THE GOLDEN GATE BRIDGE The main span of San Francisco’s Golden Gate Bridge is 1275 m long at its coldest. The bridge is exposed to temperatures ranging from –15ºC to 40ºC. What is its change in length between these temperatures? Assume that the bridge is made entirely of steel.

• Problem 13. You are looking to purchase a small piece of land in Hong Kong. The price is “only” $60,000 per square meter! The land title says the dimensions are 20m×30 m. By how much would the total price change if you measured the parcel with a steel tape measure on a day when the temperature was 20ºC above normal?

Heat and Heat Transfer

Template:Hidden begin{{#lst:Physics_equations/Equations|14-Heat_and_Heat_Transfer}}Template:Hidden end

EXAMPLE 14.9 CALCULATE THE NET HEAT TRANSFER OF A PERSON: HEAT TRANSFER BY RADIATION What is the rate of heat transfer by radiation, with an unclothed person standing in a dark room whose ambient temperature is 22.0ºC. The person has a normal skin temperature of 33.0ºC and a surface area of 1.50m2. The emissivity of skin is 0.97 in the infrared, where the radiation takes place.

• Problem 64. Calculate the temperature the entire sky would have to be in order to transfer energy by radiation at 1000W/m2 —about the rate at which the Sun radiates when it is directly overhead on a clear day. This value is the effective temperature of the sky, a kind of average that takes account of the fact that the Sun occupies only a small part of the sky but is much hotter than the rest. Assume that the body receiving the energy has a temperature of 27.0ºC.

Thermodynamics

Template:Hidden begin {{#lst:Physics_equations/Equations|15-Thermodynamics}}Template:Hidden end

Oscillatory Motion and Waves

Template:Hidden begin{{#lst:Physics_equations/Equations|16-Oscillatory_Motion_and_Waves}}Template:Hidden end

Physics of Hearing

Template:Hidden begin {{#lst:Physics_equations/Equations|17-Physics_of_Hearing}}Template:Hidden end

How do we...

...allow group work?

Permit individual work or groups of 2 or 3 people, with the understanding that I expect more from groups.

...encourage covering of most (if not all) sections?

The first seven questions start at Fluid Statics. Do one problem from each section until you get to the end (Physics of Hearing)

...permit people to set up or explain problems without doing the actual calculation?

You must do at least X problems to the "bitter end". After that, it's up to you. If you need to actually do the calculation, you will receive credit for that effort. If you don't need the practice, I will take your word for it.

...organize the feedback?

What I prefer: You hand in something every day on white typing paper, with:

1. Names on top 3/4 inch and 1/4 inch margin all around, and Public Domain statement inside.
2. I make a copy and return the original to you.
3. The rest of the course is devoted to you using this to "teach yourself the book".

Journal

Mon 26 Nov Fluid Statics and Fluid Dynamics

• It's OK to work on a spiral notebook and photocopy IF you find yourself wasting time doing it my way.
• Showed class: Buoyant Force problems 1 and 2. Defined pressure, P, as F/A where F is force and A is area. Pressure increases in depth as ρgh where ρ is mass density (mass/volume) and h is depth. Buoyant force is the net pressure force (i.e. between the top and bottom of a cylinder). It is also the weight of the displaced fluid.
• On Fluid Dynamics, you might just want to do the first problem. Other projects:

1. Simple and elementary: Describe the blowing over paper demonstration
2. Advanced: Explain why Q=Av, where Q is flow rate (volume/time), A is cross-sectional area, and v is flow rate. This is a beautiful thing to derive.

________________________________________________________________________________

Footnotes

• Physics equations

$F=Mg=m\frac{v^2}{r}$

$vT=2\pi r$