Complex Analysis/Path

Definition: Path

Let $U\subset ℂ$ be a subset. A path in $U$ is a continuous mapping with:

$\gamma :[a,b]\to U$ with $a<b$ and $a,b\in ℝ$.

Definition: Trace of a Path

The trace of a path $\gamma :[a,b]\to U$ in $U\subset ℂ$ is the image of the function $\gamma$:

$\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(\gamma ):=\gamma (t)\in ℂ|t\in [a,b]$

Definition: Closed Path

Let $\gamma :[a,b]\to U$ be a path in $U\subset ℂ$. The mapping $\gamma$ is called a closed path if:

$\gamma (a)=\gamma (b)$

Definition: Region

Let $U\subset ℂ$ be an open subset of $ℂ$. Then $U$ is called a region.

Definition: Path-Connected

Let $U\subset ℂ$ be a non-empty set.

$U$ is path-connected $:⟺{\mathrm{\forall }}_{z_1,z_2\in U}{\mathrm{\exists }}_{\gamma :[a,b]\to U}:\gamma (a)=z_1\wedge \gamma (b)=z_2\wedge Trace(\gamma )\subseteq U$

Definition: Domain

Let $G\subset ℂ$ be a non-empty subset of $ℂ$. If

$G$ is open

$G$ is path-connected

Then $G$ is called a domain in $ℂ$.

Example (Circular Paths)

Let $z_o\in ℂ$ be a complex number, and let $r>0$ be a radius. A circular path ${\gamma }_{z_o,r}:[0,2\pi ]\to ℂ$ around $z_o\in ℂ$ is defined as:

${\gamma }_{z_o,r}(t):=z_o+r\cdot e^{i\cdot t}$

Example - Paths with Ellipse as Trace

Let $z_o\in ℂ$ be a complex number, and let $a,b>0$ be the semi-axes of an ellipse. An elliptical path ${\gamma }_{z_o,a,b}:[0,2\pi ]\to ℂ$ around $z_o\in ℂ$ is defined as:

${\gamma }_{z_o,a,b}(t):=z_o+a\cdot \cos (t)+i\cdot b\cdot \sin (t)$

Gardener's Construction of an Ellipse

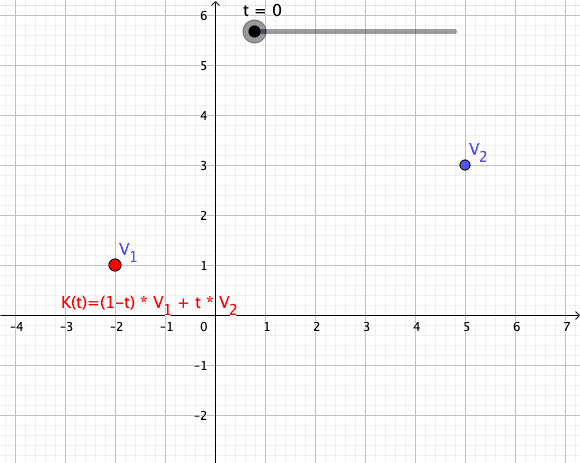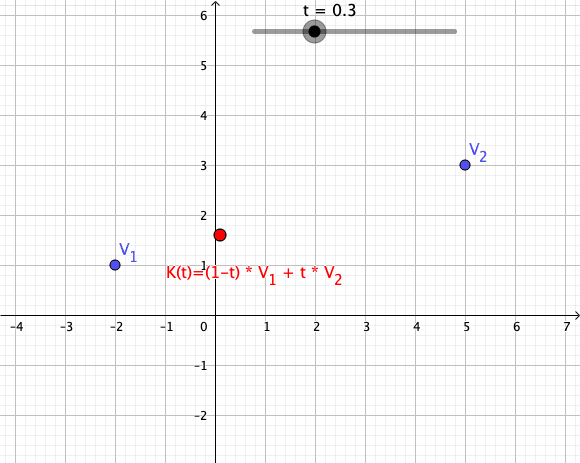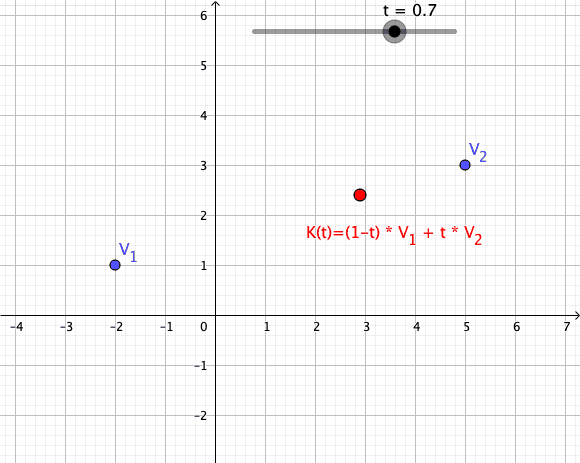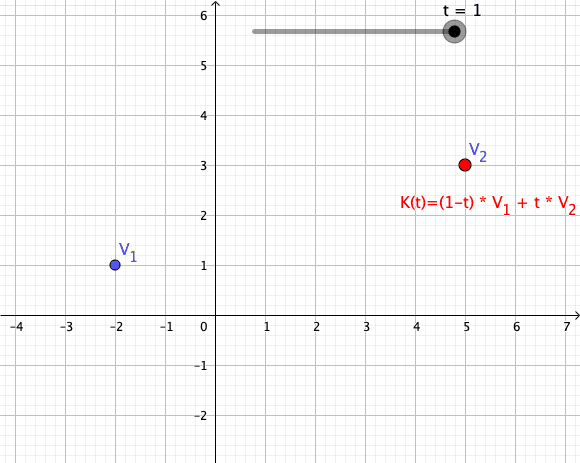
Convex Combinations

Let $z_1,z_2\in ℂ$ be complex numbers, and let $t\in [0,1]$ be a scalar. A path ${\gamma }_{z_1,z_2}:[0,1]\to ℂ$ is defined such that its trace is the line segment connecting $z_1,z_2\in ℂ$:

${\gamma }_{z_1,z2}(t):=(1-t)\cdot z_1+t\cdot z_2$

Such a path is called a convex combination of the first order (see also Higher-Order Convex Combinations).

Animation of a Convex Combination of Two Vectors as Mapping

Convex Combination as Mapping in an Animated GIF

Integration Path

Let $G\subset ℂ$ be a domain. An integration path in $G$ is a path that is piecewise continuously differentiable with

$\gamma :[a,b]\to U$ with $a<b$ and $a,b\in ℝ$.

Remark

An integration path can, for example, be expressed piecewise as convex combinations between multiple points $z_1,\dots z_n\in ℂ$. The overall path does not need to be differentiable at points $z_1,\dots z_n\in ℂ$. The trace of such a path is also called a polygonal path.

See Also

Ellipse

Convex Combination

Paths in Topological Vector Spaces

Page Information

This learning resource can be presented as a Wiki2Reveal Slide Set.

Wiki2Reveal

This Wiki2Reveal Slide Set was created for the learning unit Course: Function Theory. The link to the Wiki2Reveal Slides was generated with the Wiki2Reveal Link Generator.