Template:Physeq2

Please do not use this template. Instead go to Physics equations/Equations or a subpage and transclude from there.

• This template focuses on equations used in second semester physics.

SampleName

• Foo

<section end=SampleName/> Call with {{Physeq2|transcludesection=SampleName}}

18 Electric charge and field

ScalarElectricField

• $F=k_{\mathrm{e}}\frac{qQ}{r^2}=\frac{1}{4\pi {ϵ}_0}\frac{qQ}{r^2}$ is Coulomb's law for the force between two charged particles separated by a distance r: k_e≈8.987×10⁹N·m²·C⁻², and ε₀≈8.854×10⁻¹² F·m⁻¹.
• $\overrightarrow{F}=q\overrightarrow{E}$ is the electric force on a "test charge", q, where $E=k_{\mathrm{e}}\frac{Q}{r^2}$ is the magnitude of the electric field situated a distance r from a charge, Q.

Call with {{Physeq2|transcludesection=ScalarElectricField}}

VectorElectricField

Consider a collection of $N$ particles of charge $Q_i$, located at points ${\overrightarrow{r}}_i$ (called source points), the electric field at $\overrightarrow{r}$ (called the field point) is:

• $\overrightarrow{E}(\overrightarrow{r})=\frac{1}{4\pi {\epsilon }_0}\sum _{i=1}^N\frac{{\widehat{ℛ}}_i{Q}_i}{|{\overrightarrow{ℛ}}_i{|}^2}=\frac{1}{4\pi {\epsilon }_0}\sum _{i=1}^N\frac{{\overrightarrow{ℛ}}_i{Q}_i}{|{\overrightarrow{ℛ}}_i{|}^3}$ is the electric field at the field point, $\overrightarrow{r}$, due to point charges at the source points,${\overrightarrow{r}}_i$ , and ${\overrightarrow{ℛ}}_i=\overrightarrow{r}-{\overrightarrow{r}}_i,$ points from source points to the field point.

<section end=VectorElectricField/>

Call with {{Physeq2|transcludesection=VectorElectricField}}

VectorElectricFieldCALCULUS

• $\overrightarrow{E}(\overrightarrow{r})=k\int \frac{\widehat{ℛ}dQ}{{ℛ}^2}$ is the electric field due to distributed charge, where $dQ\to \lambda d\ell \to \sigma dA\to \rho dV$, and $(\lambda ,\sigma ,\rho )$ denote linear, surface, and volume density (or charge density), respectively. Here, Template:Nowrap begink=1/4πε_o.Template:Nowrap end

<section end=VectorElectricFieldCALCULUS/> Call with {{Physeq2|transcludesection=VectorElectricFieldCALCULUS}}

19 Electric Potential and Electric Field

DefineElectricPotential

• $U=qV$ is the potential energy of a particle of charge, q, in the presence of an electric potential V.
• $1eV=1.602\times 10^{-19}J$ is a unit of energy, defined as the work associated with moving one electron through a potential difference of one volt.
• $\mathrm{\Delta }V=-E\ell \cos \theta =\overrightarrow{E}\cdot \overrightarrow{\ell }$ (measured in Volts) is the variation in electric potential as one moves through an electric field $E$. The angle between the field and the displacement is θ. The electric potential, V, decreases as one moves parallel to the electric field.
• $\mathrm{\Delta }V=-\sum \overrightarrow{E}\cdot \mathrm{\Delta }\ell$ describes the electric potential if the field is not uniform.
• $V(\overrightarrow{r})=k\sum \frac{Q_j}{{ℛ}_j}$ due to a set of charges $Q_j$ at ${\overrightarrow{r}}_j$ where ${\overrightarrow{ℛ}}_j=\overrightarrow{r}-{\overrightarrow{r}}_j$.

<section end=DefineElectricPotential/> Call with {{Physeq2|transcludesection=DefineElectricPotential}}

Capacitors

• $Q=CV$ is the (equal and opposite) charge on the two terminals of a capacitor of capicitance, C, that has a voltage drop, V, across the two terminals.
• $C=\epsilon A/d$ is the capacitance of a parallel plate capacitor with surface area, A, and plate separation, d. This formula is valid only in the limit that Template:Nowrap begind²/ATemplate:Nowrap end vanishes. If a dielectric is between the plates, then Template:Nowrap beginε>ε₀≈ 8.85 × 10⁻¹²Template:Nowrap end due to shielding of the applied electric field by dielectric polarization effects.
• $U=\frac{1}{2}QV=\frac{1}{2}C{V}^2=\frac{Q^2}{2C}$ is the energy stored in a capacitor.
• $u=\frac{\epsilon }{2}{E}^2$ is the energy density (energy per unit volume, or Joules per cubic meter) of an electric field.

<section end=Capacitors/> Call with {{Physeq2|transcludesection=Capacitors}}

FieldTheoryCALCULUS

• $V(\overrightarrow{b})-V(\overrightarrow{a})=-\underset{\overrightarrow{a}}{\overset{\overrightarrow{b}}{\int }}\overrightarrow{E}\cdot d\ell$ in the limit that the Riemann sum becomes an integral.
• $\overrightarrow{E}=-\overrightarrow{\mathrm{\nabla }}V$ where $\overrightarrow{\mathrm{\nabla }}$ $=\hat{x}\partial /\partial x+\hat{y}\partial /\partial y+\hat{z}\partial /\partial z$ is the del operator.

<section end=FieldTheoryCALCULUS/> Call with {{Physeq2|transcludesection=FieldTheoryCALCULUS}}

VolumeSurfaceLineElements

Cartesian coordinates (x, y, z):

• $dV=dxdydz$ is a volume element
• $\hat{z}dxdy$ and $\hat{x}dydz$ and $\hat{y}dzdx$ are area elements of the form $\hat{n}dA$
• $d\overrightarrow{\ell }=\hat{x}dx+\hat{y}dy+\hat{z}dz$ is a line element.

Cylindrical coordinates (ρ, φ, z):

• $dV=\rho drd\varphi dz$ is a volume element

$=\rho d\rho dz\int d\varphi =2\pi \rho d\rho dz$ if azimuthal symmetry holds.

• $\rho d\varphi dz\hat{\rho }$ and $\rho d\rho d\varphi \hat{z}$ are surface elements in cylindrical coordinates.
• $\hat{\varphi }rd\varphi$ and $\hat{r}dr$ and $\hat{z}dz$ are line elements in cylindrical coordinates.

Spherical coordinates (r, θ, φ): Spherical symmetry holds when nothing depends on the angular variables.

• $\hat{r}dr$ is the simplest line element in spherical coordinates.
• $\hat{r}dA={\hat{r}}^{2}d\mathrm{\Omega }$ defines the solid angle. The solid angle of a sphere is 4π steradians.
• $4\pi r^{2}dr$ is the volume element of a spherical shell of radius r and thickness dr.

<section end=VolumeSurfaceLineElements/> Call with {{Physeq2|transcludesection=VolumeSurfaceLineElements}}

GradStokesDivThms

closed surfaces | Ω & ∂Ω
To the left are closed surfaces. To the right are open surfaces, Ω, that possess closed boundaries, ∂Ω.

• $\underset{\overrightarrow{p}}{\overset{\overrightarrow{q}}{\int }}\overrightarrow{\mathrm{\nabla }}f\cdot d\overrightarrow{\ell }=f(\overrightarrow{q})-f(\overrightarrow{p})$ is the gradient theorem.

• $\underset{\mathrm{\Sigma }}{\int }\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{F}\cdot \overrightarrow{dA}={\oint }_{\partial \mathrm{\Sigma }}\overrightarrow{F}\cdot d\hat{\ell }$ is Stokes' theorem

• $\underset{\mathrm{\Omega }}{\int }\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{F}dV={\oint }_{\partial \mathrm{\Omega }}\overrightarrow{F}\cdot d\overrightarrow{A}$ is the divergence theorem

Here, Ω is a (3-dimensional) volume and ∂Ω is the boundary of the volume, which is a (two-dimensional) surface. Also a surface is Σ, which, if open, has the boundary ∂Σ, which is a (one-dimensional) curve. <section end=GradStokesDivThms/> Call with {{Physeq2|transcludesection=GradStokesDivThms}}

GausslawSimple

• ${\epsilon }_0\int \overrightarrow{E}\cdot \overrightarrow{dA}=Q_{encl}$ is Gauss's law for the surface integral of the electric field over any closed surface, and $Q_{encl}$ is the total charge inside that surface. The vacuum permittivity is Template:Nowrap beginε₀≈ 8.85 × 10⁻¹²Template:Nowrap end.

<section end=GausslawSimple/> Call with {{Physeq2|transcludesection=GausslawSimple}}

Gausslaw

• ${\epsilon }_0\int \overrightarrow{E}\cdot \overrightarrow{dA}=Q_{encl}$ is Gauss's law for the surface integral of the electric field over any closed surface, and $Q_{encl}$ is the total charge inside that surface.
• $\int \overrightarrow{D}\cdot \overrightarrow{dA}=Q_{free}$ is a useful variant if the medium is dielectric. D=εE is the electric displacement field. The permittivity, Template:Nowrap beginε = (1+χ)ε₀,Template:Nowrap end where Template:Nowrap beginε₀≈ 8.85 × 10⁻¹²Template:Nowrap end, and the electric susceptibility, χ, represents the degree to which the medium can be polarized by an electric field. The free charge, Q_free, represents all charges except those represented by the susceptibility, χ.

<section end=Gausslaw/> Call with {{Physeq2|transcludesection=Gausslaw}}

20 Electric Current, Resistance, and Ohm's Law

OhmsLawResistivity

• $I=\frac{\mathrm{d}Q}{\mathrm{d}t}$ defines the electric current as the rate at which charge flows past a given point on a wire. The direction of the current matches the flow of positive charge (which is opposite the flow of electrons if electrons are the carriers.)
• $V=IR$ is Ohm's Law relating current, I, and resistance, R, to the difference in voltage, V, between the terminals. The resistance, R, is positive in virtually all cases, and if R > 0, the current flows from larger to smaller voltage. Any device or substance that obeys this linear relation between I and V is called ohmic.
• $I=nqA{v}_{drift}$ relates the density (n), the charge(q), and the average drift velocity (v_drift) of the carriers. The area (A) is measured by imagining a cut across the wire oriented such that the drift velocity is perpendicular to the surface of the (imaginary) cut.
• $R=\frac{\rho L}{A}$ expresses the resistance of a sample of ohmic material with a length (L) and area (A). The 'resistivity', ρ ("row"), is an intensive property of matter.

<section end=OhmsLawResistivity/> Call with {{Physeq2|transcludesection=OhmsLawResistivity}}

FundamentalDefinitions

• Power is energy/time, measured in joules/second or J/s. Often called P (never p). It is measured in watts (W)
• Current is charge/time, measured in coulombs/second or C/s. Often called I or i. It is measured in amps or ampheres (A)
• Electric potential (or voltage) is energy/charge, measured in joules/coulomb or J/C. Often called V (sometimes E, emf, $ℰ$). It is measured in volts (V)
• Resistance is voltage/current , measured in volts/amp or V/A. Often called R (sometimes r, Z) It is measured in Ohms (Ω).
• $P=IV=I^{2}R=\frac{V^2}{R}$ is the power dissipated as current flows through a resistor

<section end=FundamentalDefinitions/> Call with {{Physeq2|transcludesection=FundamentalDefinitions}}

21 Circuits, Bioelectricity, and DC Instruments

MiscCircuits

• $R_{\mathrm{e}\mathrm{q}}=R_1+R_2+\cdots +R_n.$ is the effective resistance for resistors in series.
• $\frac{1}{R_{\mathrm{e}\mathrm{q}}}=\frac{1}{R_1}+\frac{1}{R_2}+\cdots +\frac{1}{R_n}$ is the effective resistanc vor resistors in parallel.

voltage divider

• $\sum _{k=1}^n{I}_k=0$ and $\sum _{k=1}^n{V}_k=0$ are Kirchoff's Laws
• $V_{\mathrm{o}\mathrm{u}\mathrm{t}}=\frac{R_2}{R_1+R_2}{V}_{\mathrm{i}\mathrm{n}}$ for the voltage divider shown.

In this example, we assume that the rectangular element is a resistor, R, and that the internal resistance of the voltage source (not shown) is also R. The ammeter and voltmeter shown are ideal.

Charging and discharging a capacitor with the alternating switch shown to the left (i.e. where the RC rise and discharge times are equal).

• Simple RC circuit The figure to the right depicts a capacitor being charged by an ideal voltage source. If, at t=0, the switch is thrown to the other side, the capacitor will discharge, with the voltage, V , undergoing exponential decay:

$V(t)=V_0{e}^{-\frac{t}{RC}},$

where V₀ is the capacitor voltage at time t = 0 (when the switch was closed). The time required for the voltage to fall to $\frac{V_0}{e}\approx .37V_0$ is called the RC time constant and is given by

$\tau =RC.$

<section end=MiscCircuits/> Call with {{Physeq2|transcludesection=MiscCircuits}}

22 Magnetism

VectorMagneticForce

• $F=qvB\sin \theta$ is the force on a particle with charge q moving at velocity v with in the presence of a magnetic field B. The angle between velocity and magnetic field is θ and the force is perpeduclar to both velocity and magnetic field by the right hand rule.
• $\overrightarrow{F}=q\overrightarrow{v}\times \overrightarrow{B}$ expresses this result as a cross product.
• $\mathrm{\Delta }\overrightarrow{F}=I\mathrm{\Delta }\overrightarrow{\ell }\times \overrightarrow{B}$ is the force a straight wire segment of length $\mathrm{\Delta }\ell$ carrying a current, I.
• $\overrightarrow{F}=I\sum \mathrm{\Delta }\ell \times \overrightarrow{B}$ expresses thus sum over many segments to model a wire.
• CALCULUS: In the limit that $\mathrm{\Delta }\ell \to 0$ we have the integral, $\overrightarrow{F}=I\oint d\ell \times \overrightarrow{B}$.

<section end=VectorMagneticForce/> Call with {{Physeq2|transcludesection=VectorMagneticForce}}

DefineMagneticFieldVector

• $\mathrm{\Delta }\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\frac{I\mathrm{\Delta }\overrightarrow{\ell }\times \hat{r}}{|r{|}^2}$ is the contribution to the field due to a short segment of length $\mathrm{\Delta }\ell$ carrying a current I, where the displacement vector r points from the source point to the field point.

<section end=DefineMagneticFieldVector/> Call with {{Physeq2|transcludesection=DefineMagneticFieldVector}}

DefineMagneticFieldVectorCALCULUS

• $\overrightarrow{B}=\oint \frac{{\mu }_0}{4\pi }\frac{Id\overrightarrow{\ell }\times \hat{r}}{|r{|}^2}$ and the volume integral $\int \frac{{\mu }_0}{4\pi }\frac{\overrightarrow{J}\times \hat{r}}{|r{|}^2}d{\tau }^{\prime }$, where $\overrightarrow{J}$ is current density.
• $\oint 𝐁\cdot \mathrm{d}𝐥={\mu }_0{I}_{encl}$ is Ampere's law relating a closed integral involving magnetic field to the total current enclosed by that path.

<section end=DefineMagneticFieldVectorCALCULUS/> Call with {{Physeq2|transcludesection=DefineMagneticFieldVectorCALCULUS}}

DefineMagneticFieldScalar

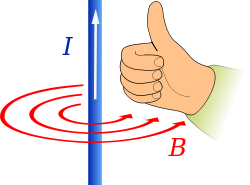
1.   $B=\frac{{\mu }_{0}I}{2\pi r}$ is the magnetic field at a distance r from an infinitely long wire carrying a current, where Template:Nowrap beginμ₀ =Template:Nowrap end Template:Nowrap begin4π × 10⁻⁷ N ATemplate:Nowrap end. This field points azimuthally around the wire in a direction defined by the right hand rule. Application of the force law on a current element, we have
2.   $F=\frac{{\mu }_0{I}_1{I}_2\ell }{2\pi r}$ is the force between two long wires of length $\ell$ separated by a short distance $r<<\ell$. The currents are I₁ and I₂, with the force being attractive if the currents are flowing in the same direction.

<section end=DefineMagneticFieldScalar/> Call with {{Physeq2|transcludesection=DefineMagneticFieldScalar}}These equations are exact in that they serve to define both μ₀ as well a the ampere.

CyclotronMotion

For a particle moving perpendicular to B, we have cyclotron motion. Recall that for uniform circular motion, the acceleration is a=v²/r, where r is the radius. Since sin θ =1, Newton's second law of motion (F=ma) yields,

$ma=\frac{m{v}^2}{r}=qvB$

Since, sin θ =0, for motion parallel to a magnetic field, particles in a uniform magnetic field move in spirals at a radius which is determined by the perpendicular component of the velocity:

$r=\frac{m{v}_{\perp }}{qB}$

<section end=CyclotronMotion/> Call with {{Physeq2|transcludesection=CyclotronMotion}}

HallEffect

The Hall effect occurs when the magnetic field, velocity, and electric field are mutually perpendicular. In this case, the electric and magnetic forces are aligned, and can cancel if qE=qvB (since sinθ = 1). Since both terms are porportional to charge, q, the appropriate ratio of electric to magnetic field for null net force depends only on velocity:

$E=vB=\frac{\mathrm{e}\mathrm{m}\mathrm{f}}{\ell }$,

where we have used the fact that voltage (i.e. emf or potential) is related to the electric field and a displacement parallel to that field: ΔV = -E Δs cosθ

<section end=HallEffect/> Call with {{Physeq2|transcludesection=HallEffect}}

23 Electromagnetic Induction, AC Circuits, and Electrical Technologies

FaradayLaw

In rod's frame the force on carriers is electric, not magnetic. (See railgun)

• $\overrightarrow{E}=\overrightarrow{v}\times \overrightarrow{B}$ is a consequence of the magnetic force law as seen in the reference frame of a moving charged object, where E is the electric field perceived by an observer moving at velocity v in the presence of a magnetic vield, B. Also written as, Template:Nowrap beginE = vBsinθTemplate:Nowrap end, this can be used to derive Faraday's law of induction. (Here, θ is the angle between the velocity and the magnetic field.)
• $\mathrm{\Phi }=\overrightarrow{A}\cdot \overrightarrow{B}=AB\cos \theta$ is the magnetic flux, where θ is the angle between the magnetic field and the normal to a surface of area, A.
• $emf=-N\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$ is Faraday's law where t is time and N is the number of turns. The minus sign reminds us that the emf, or electromotive force, acts as a "voltage" that opposes the change in the magnetic field or flux.

<section end=FaradayLaw/> Call with {{Physeq2|transcludesection=FaradayLaw}}

24 Electromagnetic Waves

DisplacementCurrent

• ${ϵ}_0\partial \overrightarrow{E}/\partial t$ is called the displacement current because it replaces the current density when using Ampère's circuital law to calculate the line integral of the magnetic field around a closed loop.

<section end=DisplacementCurrent/> Call with {{Physeq2|transcludesection=DisplacementCurrent}}

25 Geometric Optics

ThinLensEquation

$\frac{1}{S_1}+\frac{1}{S_2}=\frac{1}{f}$ relates the focal length f of the lens, the image distance S₁, and the object distance S₂. The figure depicts the situation for which Template:Nowrap are all positive: (1)The lens is converging (convex); (2) The real image is to the right of the lens; and (3) the object is to the left of the lens. If the lens is diverging (concave), then f < 0. If the image is to the left of the lens (virtual image), then S₂ < 0 .
Call with {{Physeq2|transcludesection=ThinLensEquation}}

27 Wave Optics

InterferenceDiffraction

• $S\sin \theta =n\lambda$ where $n=1,2,3,4...$ describes the constructive interference associated with two slits in the Fraunhoffer (far field) approximation.

<section end=InterferenceDiffraction/> Call with {{Physeq2|transcludesection=InterferenceDiffraction}}

Beats

• $\cos \left({\omega }_{1}t\right)+\cos \left({\omega }_{2}t\right)=A(t)\cos \left(\overline{\omega }t\right)$ where $\overline{\omega }$ is the high frequency carrier and $A(t)=2\cos \left(\frac{\mathrm{\Delta }\omega }{2}t\right)$ is the slowly varying envelope. Here,

$\overline{\omega }=\frac{{\omega }_1+{\omega }_2}{2}$ and $\mathrm{\Delta }\omega ={\omega }_2-{\omega }_1$. Consequently, the beat frequency heard when two tones of frequency $f_1$ and $f_2$ is $\mathrm{\Delta }f=f_2-f_1$.

• $cos(k{\ell }_1-\omega t)+cos(k{\ell }_2-\omega t)=2cos\left(k\mathrm{\Delta }\ell \right)\cos (\omega t-\varphi )$ models the addition of two waves of equal amplitude but different path length, $\mathrm{\Delta }\ell ={\ell }_2-{\ell }_1$.

<section end=Beats/> Call with {{Physeq2|transcludesection=Beats}}