Distances/Vectors

In mathematics and physics, a vector is a quantity having direction as well as magnitude, especially as determining the position of one point in space relative to another.

Theoretical classical mechanics

Def. an "[amount of] intervening space between two points, usually geographical points, usually (but not necessarily) measured along a straight line" is called a distance.

Def. the "inevitable progression into the future with the passing of present events into the past" or the "inevitable passing of events from future to present then past" is called time.

Def. the "quantity of matter which a body contains, irrespective of its bulk or volume" or a "quantity of matter cohering together so as to make one body, or an aggregation of particles or things which collectively make one body or quantity" is called a mass.

Def. the "rate of motion or action, specifically the magnitude of the velocity; the rate distance is traversed in a given time" is called the speed.

Theoretical vectors

Def.

1. "a quantity that has both magnitude and direction"
2. "the signed difference between two points" or
3. an "ordered tuple representing a directed quantity or the signed difference between two points"

is called a vector.

Unit vectors

Notation: let $\hat{i}$ denote a unit vector in the ith direction.

Def. a "vector with length 1" is called a unit vector

Force vectors

The diagram breaks down a force vector relative to coordinate axes x and y. Credit: HUB.

A force vector is a force defined in two or more dimensions with a component vector in each dimension which may all be summed to equal the force vector. Similarly, the magnitude of each component vector, which is a scalar quantity, may be multiplied by the unit vector in that dimension to equal the component vector.

$\overrightarrow{F}={\overrightarrow{F}}_x+{\overrightarrow{F}}_y+{\overrightarrow{F}}_z=F_x\hat{i}+F_y\hat{j}+F_z\hat{k},$

where $F_x$ is the magnitude of the force in the ith direction parallel to the x-axis. Template:Clear

Triclinic coordinate systems

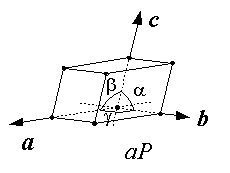
A triclinic coordinate system has coordinates of different lengths (a ≠ b ≠ c) along x, y, and z axes, respectively, with interaxial angles that are not 90°. The interaxial angles α, β, and γ vary such that (α ≠ β ≠ γ). These interaxial angles are α = y⋀z, β = z⋀x, and γ = x⋀y, where the symbol "⋀" means "angle between". Template:Clear

Monoclinic coordinate systems

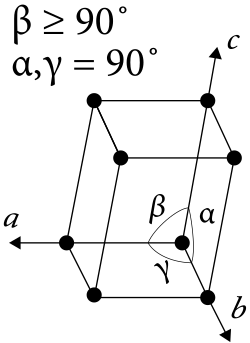
In a monoclinic coordinate system, a ≠ b ≠ c, and depending on setting α = β = 90° ≠ γ, α = γ = 90° ≠ β, α = 90° ≠ β ≠ γ, or α = β ≠ γ ≠ 90°. Template:Clear

Orthorhomic coordinate systems

In an orthorhombic coordinate system α = β = γ = 90° and a ≠ b ≠ c. Template:Clear

Tetragonal coordinate systems

A tetragonal coordinate system has α = β = γ = 90°, and a = b ≠ c. Template:Clear

Rhombohedral coordinate systems

A rhombohedral system has a = b = c and α = β = γ < 120°, ≠ 90°. Template:Clear

Hexagonal coordinate systems

A hexagonal system has a = b ≠ c and α = β = 90°, γ = 120°. Template:Clear

Cubic coordinate systems

A Hexahedron is a cube; a regular polyhedron. Credit: Kjell André.

A cubic coordinate system has a = b = c and α = β = γ = 90°.

For two points in cubic space (x₁, y₁, z₁) and (x₂, y₂, z₂), with a vector from point 1 to point 2, the distance between these two points is given by

$d=\sqrt{(\mathrm{\Delta }x{)}^2+(\mathrm{\Delta }y{)}^2+(\mathrm{\Delta }z{)}^2}=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2+(z_2-z_1{)}^2}.$

Hypotheses

1. For a vector, the direction can be stated and the magnitude is arbitrary.

See also

• A-Level Mechanics - Vectors
• Force systems
• Unknown coordinate systems
• Vectors and coordinates