Wright State University Lake Campus/University Physics Volume 1/Equations

OpenStax equations/Guild/A

User:Guy vandegrift/T/Courses now

Template:Green WSU Lake Template:Green

Math

radian&arclength

unit vectors

Metric prefixes on page 5.

Template:Clear Template:Colbegin ▭ Arclength $s$ ▭  $r$ radius
▭ $\theta =s/r$ (in radians)
▭ $C_{\odot }=2\pi r$ Circumference of circle
▭ $A_{\odot }=\pi r^2$ Area of circle
▭ $A_{◯}=4\pi r^2$ Area of sphere
▭ $V_{◯}=\frac{4}{3}\pi r^3$ Volume of sphere
▭ $\overrightarrow{ℱ}\cdot d\overrightarrow{s}$$={ℱ}_{x}dx+{ℱ}_{y}dy={ℱ}_{r}dr+{ℱ}_{\theta }rd\theta$

Mechanics

Symbols

Template:Colbegin ▭ $\overrightarrow{r}=x\hat{i}+y\hat{j}+z\hat{k}=x\hat{x}+y\hat{y}+z\hat{z}$ Position
▭ $\mathrm{\Delta }\overrightarrow{\ell },d\overrightarrow{\ell },\mathrm{\Delta }\overrightarrow{s},d\overrightarrow{s}$ Line element (better than $d\overrightarrow{r}$)
▭ $\overrightarrow{v}=d\overrightarrow{r}/dt$ Velocity [m/s]
▭ $\overrightarrow{a}=d\overrightarrow{v}/dt$ Acceleration [m/s]
▭ $\overrightarrow{F}=m\overrightarrow{a}$ Force [N], Mass [kg], Acceleration [m/s²]
▭ $f$ Friction force [N] or frequency [Hz=s⁻¹]
▭ ${\mu }_{s,k}$ (static, kinetic) coefficient of friction
▭ $\overrightarrow{N}$ normal force
▭ $g$ gravitational constant (Earth: 9.8m/s²)
Template:Green G≈Template:Val
▭ $W$ Work [J=Nm=kg(m/s)²]
▭ $P$ Power [W=J/s]
▭ $\overrightarrow{p}$ Momentum
▭ $p$ Pressure (N/m²)
▭ $KE(PE)$ Kinetic (Potential) Energy [J=Nm=Ws]
▭ $(U_g,U_s)$ Potential energy (gravity, spring)
▭ $F=-k_{s}x$ defines spring constant [N/m]
▭ $T$ Tension [N] or period [s] or temperature [K]
▭ $Q$ Heat [J=Ws]
▭ $\theta$ Angle (radians)
▭ $\omega =d\theta /dt$ Angular velocity (speed) [s⁻¹]
▭ $\alpha =d\omega /dt$ Angular acceleration [s⁻²]
▭ $I=\mathrm{\Sigma }{m}_i{r}_i^2$ Moment of inertia
▭ $\tau =I\alpha$ Torque ▭$L=I\omega$ Angular momentum
Template:Colend Template:Clear

Kinematics

Linear motion	Rotational motion	Defining equation
Displacement = $𝐱$	Angular displacement = $\theta$	$\theta =𝐬/𝐫$
Velocity = $𝐯$	Angular velocity = $\omega$	$\omega =𝐝\theta /𝐝𝐭=𝐯/𝐫$
Acceleration = $𝐚$	Angular acceleration = $\alpha$	$\alpha =𝐝\omega /𝐝𝐭={𝐚}_{𝐭}/𝐫$
Mass = $𝐦$	Moment of Inertia = $𝐈$	$𝐈=\sum {𝐦}_{𝐣}{{𝐫}_{𝐣}}^2$
Force = $𝐅=𝐦𝐚$	Torque = $\tau =𝐈\alpha$	$\tau =\sum {𝐫}_{𝐣}{𝐅}_{\perp }{}_{𝐣}=\sum {𝐫}_{\mathbf{\perp }𝐣}{𝐅}_{{}_{𝐣}}$
Momentum= $𝐩=𝐦𝐯$	Angular momentum= $𝐋=𝐈\omega$	$𝐋=\sum {𝐫}_{𝐣}𝐩{}_{𝐣}$
Kinetic energy = $\frac{1}{2}𝐦{𝐯}^2$	Kinetic energy = $\frac{1}{2}𝐈{\omega }^2$	$\frac{1}{2}\sum {𝐦}_{𝐣}{{𝐯}_{𝐣}}^2=\frac{1}{2}\sum {𝐦}_{𝐣}{{𝐫}_{𝐣}}^2{\omega }^2$

Vector notation	Component notation
$\overrightarrow{r}-{\overrightarrow{r}}_0={\overrightarrow{v}}_{0}t+\frac{1}{2}\overrightarrow{a}{t}^2$	${\overrightarrow{v}}_0={\overrightarrow{v}}_{0x}\hat{i}+{\overrightarrow{v}}_{0y}\hat{j}+{\overrightarrow{v}}_{0z}\hat{k}$
$v^2=v_0^2+2\overrightarrow{a}\cdot (\overrightarrow{r}-{\overrightarrow{r}}_0)$	Free fall: $a_x=0,a_y=-g$

Linear motion	Angular motion
$x-x_0=v_{0}t+\frac{1}{2}a{t}^2$	$\theta -{\theta }_0={\omega }_{0}t+\frac{1}{2}\alpha t^2$
$v=v_0+at$	$\omega ={\omega }_0+\alpha t$
$x-x_0=\frac{1}{2}(v_0+v)t$	$\theta -{\theta }_0=\frac{1}{2}({\omega }_0+\omega )t$
$v^2=v_0^2+2a(x-x_0)$	${\omega }^2={\omega }_0^2+2\alpha (\theta -{\theta }_0)$

Equations

Template:Colbegin ▭ $KE=\frac{1}{2}m{v}^2$  ▭ $U_g=mgy+𝒞$  ▭ $U_s=\frac{1}{2}{k}_s{x}^2$
▭ $\sum K{E}_f+\sum P{E}_f=\sum K{E}_i+\sum P{E}_i-Q$
▭ $W=F\ell \cos \theta =\overrightarrow{F}\cdot \overrightarrow{\ell }\Rightarrow \sum \overrightarrow{F}\cdot \mathrm{\Delta }\ell \Rightarrow \int \overrightarrow{F}\cdot \mathrm{\Delta }\ell$
▭ $P=\frac{\overrightarrow{F}\cdot \overrightarrow{\mathrm{\Delta }}\ell }{\mathrm{\Delta }t}=\overrightarrow{F}\cdot \overrightarrow{v}$ is power
▭ $\overrightarrow{p}=m\overrightarrow{v}$ Momentum
▭ $\sum {\overrightarrow{p}}_f=\sum {\overrightarrow{p}}_f+\int {\overrightarrow{F}}_{ext}dt$
▭ $m_1{v}_1+m_2{v}_2=(m_1+m_2)v_f$ Inelastic collision
▭ $\omega T=2\pi \iff fT=1$ frequency-period
▭ $a=v^2/r=\omega v={\omega }^{2}r$ centripetal acceleration
▭ $\sum {\overrightarrow{F}}_j=0=\sum {\overrightarrow{\tau }}_j$ $\tau =r{F}_{\perp }$ statics
▭ $f_s\le {\mu }_{s}N,f_k={\mu }_{k}N$ friction
▭ ${\overrightarrow{F}}_{12}=G\frac{m_1{m}_2}{r^2}{\hat{r}}_{12}$ Newtonian gravity
▭ ${\overrightarrow{F}}_{12}=G\frac{m_1{m}_2}{r^2}{\hat{r}}_{12}$Newtonian gravity
▭ $g=G\frac{M}{r^2}$ planet's surface gravity
Template:Colend

Fluid_Mechanics

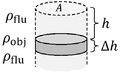
Pressure is the weight per unit area of the fluid above a point.

▭ Mass density $\rho =m/V$

▭ Pressure $P=F/A$

Buoyant force $B$ equals weight of the displaced fluid. If $W$ is the weight of a cylindrical object, the displaced volume is $A\mathrm{\Delta }h$

Template:Spaces▭ $B={\rho }_{flu}(A\mathrm{\Delta }h)g$ and ▭ $W={\rho }_{obj}(A\mathrm{\Delta }h)g=M_{obj}g$

▭ Pressure vs depth/height (constant density)$p=p_o+\rho gh\Leftarrow dp/dy=-\rho g$

▭ Volume flow rate $Q=dV/dt$

▭ Continuity equation ${\rho }_1{A}_1{v}_1={\rho }_2{A}_2{v}_2$$\Rightarrow A_1{v}_1=A_2{v}_2\text{ if }\rho =const.$

▭ Bernoulli's principle $p_1+\frac{1}{2}\rho v_1^2+\rho g{y}_1=p_2+\frac{1}{2}\rho v_2^2+\rho g{y}_2$

Oscillations

▭ Simple harmonic motion $x(t)=A\cos (\omega t+\varphi ),$ $v(t)=-A\omega \sin (\omega t+\varphi ),$ $a(t)=-A{\omega }^2\cos (\omega t+\varphi )$

▭ $x_{max}=A,v_{max}=A\omega ,a_{max}=A{\omega }^2$, where $\omega =\sqrt{k/m};$ and $k$ is spring constant

▭ Energy $E_{Tot}=\frac{1}{2}k{x}^2+\frac{1}{2}m{v}^2=\frac{1}{2}m{v}_{max}^2=\frac{1}{2}k{x}_{max}^2$

Template:Green

• $v_s=\sqrt{\frac{T}{273}}\cdot 331\text{m/s}$ speed of sound (T in Kelvins). $v_s=\sqrt{\frac{\gamma k_{B}T}{m}}$ where $\gamma \approx 1.4$
• $v=\sqrt{\frac{F}{\mu }}$ Speed of a stretched string wave: $F$ is the tension and $\mu$ is the linear mass density (kilograms per meter).

• $f\lambda =v_p$ relates the frequency, f, wavelength, λ,and the the phase speed, v_p of the wave (also written as v_w) This phase speed is the speed of individual crests, which for sound and light waves also equals the speed at which a wave packet travels.
• $L=\frac{n{\lambda }_n}{2}$ describes the n-th normal mode vibrating wave on a string that is fixed at both ends (i.e. has a node at both ends). The mode number, n = 1, 2, 3,..., as shown in the figure.
• Beat frequency: The frequency of beats heard if two closely space frequencies, $f_1$ and $f_2$, are played is $\mathrm{\Delta }f=|f_2-f_1|$.
• Musical acoustics: Frequency ratios of 2/1, 3/2, 4/3, 5/3, 5/4, 6/5, 8/5 are called the (just) "octave", "fifth", "fourth", "major-sixth", "major-third", "minor-third", and "minor-sixth", respectively.

Thermodynamics

Constants and conversions

• Boltzmann's constant = k_B≈ Template:Nowrap, and the gas constant is R = Template:Nowrap≈Template:Nowrap, where N_A≈ Template:Nowrap is the Avogadro number.
• Boltzmann's constant can also be written in eV and Kelvins: k_B ≈Template:Nowrap, where Template:Nowrap begin1eV=1.602x10⁻¹⁹ JoulesTemplate:Nowrap end
• $T_C=T_K-273.15$ converts from Celsius to Kelvins, and $T_F=\frac{9}{5}{T}_C+32$ converts from Celsius to Fahrenheit.
• 1 amu = 1 u ≈ 1.66 × 10^-27 kg is the approximate mass of a proton or neutron.

13-Temperature, Kinetic Theory, and Gas Laws

• $PV=nRT=N{k}_{B}T$ is the ideal gas law, where P is pressure, V is volume, n is the number of moles and N is the number of atoms or molecules. Temperature is in Kelvins.

• $\frac{3}{2}{k}_{B}T=\frac{1}{2}m{v}_{rms}^2$ is the average translational kinetic energy per "atom" of a 3-dimensional ideal gas.
• $v_{rms}=\sqrt{\frac{3k_{B}T}{m}}=\sqrt{\overline{v^2}}$ is the root-mean-square speed of atoms in an ideal gas.

14-Heat and Heat Transfer

<section begin=14-Heat_and_Heat_Transfer/> Here it is convenient to define heat as energy that passes between two objects of different temperature $Q$ The SI unit is the Joule. The rate of heat trasfer, $\mathrm{\Delta }Q/\mathrm{\Delta }t$ or $\dot{Q}$ is "power": Template:Nowrap begin1 Watt = 1 W = 1J/sTemplate:Nowrap end

• $Q=m{c}_S\mathrm{\Delta }T$ is the heat required to change the temperature of a substance of mass, m. The change in temperature is ΔT. The specific heat, c_S, depends on the substance (and to some extent, its temperature and other factors such as pressure). Heat is the transfer of energy, usually from a hotter object to a colder one. The units of specfic heat are energy/mass/degree, or Template:Nowrap beginJ/(kg-degree)Template:Nowrap end.
• $Q=mL$ is the heat required to change the phase of a a mass, m, of a substance (with no change in temperature). The latent heat, L, depends not only on the substance, but on the nature of the phase change for any given substance. L_F is called the latent heat of fusion, and refers to the melting or freezing of the substance. L_V is called the latent heat of vaporization, and refers to evaporation or condensation of a substance.
• $\dot{Q}=\frac{k_{c}A}{d}\mathrm{\Delta }T$ is rate of heat transfer for a material of area, A. The difference in temperature between two sides separated by a distance, d, is $\mathrm{\Delta }T$. The thermal conductivity, k_c, is a property of the substance used to insulate, or subdue, the flow of heat.

15-Thermodynamics

• Here, Pressure (P), Energy (E), Volume (V), and Temperature (T) are the state functions.

• The net work done per cycle is the area enclosed by the loop and equals the net heat flow into the system, $Q_{in}-Q_{out}$ (valid only for closed loops).
• $\mathrm{\Delta }W=-F\mathrm{\Delta }x=(-P\cdot \mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a})\left(\frac{\mathrm{\Delta }V}{\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}}\right)=-P\mathrm{\Delta }V$ is the work done on a system of pressure P by a piston of voulume V. If ΔV>0 the substance is expanding as it exerts an outward force, so that ΔW<0 and the substance is doing work on the universe; ΔW>0 whenever the universe is doing work on the system.
• $\mathrm{\Delta }Q$ is the amount of heat (energy) that flows into a system. It is positive if the system is placed in a heat bath of higher temperature. If this process is reversible, then the heat bath is at an infinitesimally higher temperature and a finite ΔQ takes an infinite amount of time.
• $\mathrm{\Delta }E=\mathrm{\Delta }Q-P\mathrm{\Delta }V$ is the change in energy (First Law of Thermodynamics).
• $-\int PdV$ is work done on system. $\oint PdV=Q_{in}-Q_{out}$ is work (out) per cycle.

Original (long) formula sheet

{{#lst:OpenStax University Physics Volume 1/Equations (master)|Introduction}}

1. Template:Green $C_{\odot }=2\pi r$ and the circle's area is $A_{\odot }=\pi r^2$ is its area.
2. The surface area of a sphere is $A_{◯}=4\pi r^2$ and sphere's volume is $V_{◯}=\frac{4}{3}\pi r^3$
3. Template:Green = .621 miles and 1 MPH = 1 mi/hr ≈ .447 m/s
4. Template:Green is 1.2kg/m³, with pressure 10⁵Pa. The density of water is 1000kg/m³.
5. Template:GreenTemplate:Val
6. Template:Green = G ≈ Template:Val
7. Template:Green = c ≈ 3×10⁸m/s
8. Template:Green
9. Template:Green.... <These 8 equations were added for WSU-L exams>

{{#lst:OpenStax University Physics Volume 1/Equations (master)|Units_and_Measurement}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Vectors}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Motion_Along_a_Straight_Line}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Motion_in_Two_and_Three_Dimensions}}

Template:Green

$x=x_0+v_{0x}\mathrm{\Delta }t+\frac{1}{2}{a}_x\mathrm{\Delta }{t}^2$	Template:Spaces$v_x=v_{0x}+a_x\mathrm{\Delta }t$	Template:Spaces$v_x^2=v_{x0}^2+2a_x\mathrm{\Delta }x$
$y=y_0+v_{0y}\mathrm{\Delta }t+\frac{1}{2}{a}_y\mathrm{\Delta }{t}^2$	Template:Spaces$v_y=v_{0y}+a_y\mathrm{\Delta }t$	Template:Spaces$v_y^2=v_{x0}^2+2a_y\mathrm{\Delta }y$

$v^2=v_0^2+2a_x\mathrm{\Delta }x+2a_y\mathrm{\Delta }y$   ...in advanced notation this becomes $\mathrm{\Delta }(v^2)=2\overrightarrow{a}\cdot \mathrm{\Delta }\overrightarrow{\ell }$.

In free fall we often set, a_x=0 and a_y= -g. If angle is measured with respect to the x axis:

$v_x=v\cos \theta$ Template:Spaces$v_y=v\sin \theta$ Template:Spaces$v_{x0}=v_0\cos {\theta }_0$ Template:Spaces$v_{y0}=v_0\sin {\theta }_0$

{{#lst:OpenStax University Physics Volume 1/Equations (master)|Newton's_Laws_of_Motion}}

Template:Green this quiz

{{#lst:OpenStax University Physics Volume 1/Equations (master)|Applications_of_Newton's_Laws}}

$T_{1x}=-T_1\cos {\theta }_1$ ,        $T_{1y}=T_1\sin {\theta }_1$

$T_{2x}=0$ ,                             $T_{2y}=-mg$

$T_{3x}=T_3\cos {\theta }_3$ ,          $T_{3y}=T_3\sin {\theta }_3$

• $2\pi rad=360deg=1rev$ relates the radian, degree, and revolution.
• $f=\frac{\mathrm{\#}\text{revs}}{\mathrm{\#}\text{secs}}$ is the number of revolutions per second, called frequency.
• $T=\frac{\mathrm{\#}\text{secs}}{\mathrm{\#}\text{revs}}$ is the number of seconds per revolution, called period. Obviously $fT=1$.
• $\omega =\frac{\mathrm{\Delta }\theta }{\mathrm{\Delta }t}$ is called angular frequency (ω is called omega, and θ is measured in radians). Obviously $\omega T=2\pi$
• $a=\frac{v^2}{r}=\omega v={\omega }^{2}r$ is the acceleration of uniform circular motion, where v is speed, and r is radius.
• $v=\omega r=2\pi r/T$, where T is period.

{{#lst:OpenStax University Physics Volume 1/Equations (master)|Work_and_Kinetic_Energy}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Potential_Energy_and_Conservation_of_Energy}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Linear_Momentum_and_Collisions}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Fixed-Axis_Rotation}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Angular_Momentum}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Static_Equilibrium_and_Elasticity}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Gravitation}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Fluid_Mechanics}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Oscillations}} {{#lst:OpenStax University Physics Volume 1/Equations (master)|Waves}}

Template:Green

Pressure and displacement fluctuations in a sound wave $P=\mathrm{\Delta }{P}_{max}\sin (kx\mp \omega t+\varphi )$ and $s=s_{max}\cos (kx\mp \omega t+\varphi )$

▭ Speed of sound in a fluid $v=f\lambda =\sqrt{\beta /\rho }$, ▭ in a solid $\sqrt{Y/\rho }$, ▭ in an idal gas $\sqrt{\gamma RT/M}$, ▭ in air $331\frac{m}{s}\sqrt{\frac{T_K}{273K}}=331\frac{m}{s}\sqrt{1+\frac{T_C}{273^{o}C}}$

Template:Green

{{#lst:Physics_equations/Equations|17-Physics_of_Hearing}}

• $f\lambda =v_p$ relates the frequency, f, wavelength, λ,and the the phase speed, v_p of the wave (also written as v_w) This phase speed is the speed of individual crests, which for sound and light waves also equals the speed at which a wave packet travels.
• $L=\frac{n{\lambda }_n}{2}$ describes the n-th normal mode vibrating wave on a string that is fixed at both ends (i.e. has a node at both ends). The mode number, n = 1, 2, 3,..., as shown in the figure.
• Beat frequency: The frequency of beats heard if two closely space frequencies, $f_1$ and $f_2$, are played is $\mathrm{\Delta }f=|f_2-f_1|$.
• Musical acoustics: Frequency ratios of 2/1, 3/2, 4/3, 5/3, 5/4, 6/5, 8/5 are called the (just) "octave", "fifth", "fourth", "major-sixth", "major-third", "minor-third", and "minor-sixth", respectively.

Template:Green

• $T_C=T_K-273.15$ converts from Celsius to Kelvins, and $T_F=\frac{9}{5}{T}_C+32$ converts from Celsius to Fahrenheit.
• $PV=nRT=N{k}_{B}T$ is the ideal gas law, where $P$ is pressure, $V$ is volume, $n$ is the number of moles and $N$ is the number of atoms or molecules. Temperature must be measured on an absolute scale (e.g. Kelvins).
• Boltzmann's constant = $k_B$≈ Template:Nowrap, and the gas constant is $R=N_A{k}_B$ ≈Template:Nowrap, where $N_A$≈ Template:Nowrap is the Avogadro number. Boltzmann's constant can also be written in eV and Kelvins: k_B ≈Template:Nowrap.
• $\frac{3}{2}{k}_{B}T=\frac{1}{2}m{v}_{rms}^2$ is the average translational kinetic energy per "atom" of a 3-dimensional ideal gas.
• $v_{rms}=\sqrt{\frac{3k_{B}T}{m}}=\sqrt{\overline{v^2}}$ is the root-mean-square speed of atoms in an ideal gas.
• $E=\frac{\varpi }{2}N{k}_{B}T$ is the total energy of an ideal gas, where $\varpi =3$ only if the gas is monatomic.

Template:Green

{{#lst:Physics_equations/Equations|15-Thermodynamics}}