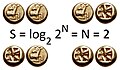Physics/A/Shannon entropy

Simple information entropy

$2^S=\mathrm{\Omega }\leftrightarrow S={\log }_2\mathrm{\Omega }$

# coins $S$ Entropy	# messages $\mathrm{\Omega }$ Omega
$2$	$4=2^2=2\cdot 2$
$3$	$8=2^3=2\cdot 2\cdot 2$
$4$	$16=2^4$
$5$	$32=2^5$
Table 1: More than two coins $S$= entropy; $\mathrm{\Omega }$= the number of possible messages

Fig. 1: Entropy of 2 coins

Figure 2. Elephant with 5 bits of entropy can give 3 bits to Bird and 2 bits to Rat.

Figure 3: Rat could display the same information using a single 4-sided die.

Figure 1 illustrates the fact that flipping two coins can yield four get four different outcomes (represented as four pairs of flipped coins.) Using (Template:Math,Template:Math) to represent (heads,tails) we can list these four outcomes,

Template:Spaces Template:Math, Template:Math, Template:Math, and Template:Math,

We shall use the symbol Template:Math (Omega) to denote the number of messages that can be sent by these two coins:

Template:Spaces Template:Math

The popularity of this inspired me to seek other ways to use coins to understand what is known as Shannon's entropy. Table 1 extends Figure 1 to include the relationship between entropy $S$ and the number of messages $\mathrm{\Omega }$ (called Omega) one might generate by displaying Template:Math coins as either "heads" or "tails". But neither the table, the figure, nor even the formula,

Template:Spaces$S=lo{g}_2\mathrm{\Omega },$

captures the full complexity associated with Shannon's information entropy. A hint at this complexity can be seen in the following question:

If entropy is equivalent to the number of coins used to convey information, how should one deal with a "one-sided coin?

Such a question must be viewed outside the scope of mathematics. The fact that one rarely hears "fire!" in a crowded theater does not remove that word from the lexicon of how the audience should behave in a theater. If coins<rev>i.e. a base-1 "alphabet"</ref> Shannon's entropy, $H,$ was defined so coins contribute nothing to the entropy

Define S as simple entropy and note that it is the number of "coins" used. Shanon's entropy, H, defined so that it also depends on the probability with which a coin is used. Connect probability to frequency.

$H\le S=N$

Additive property I

Figure 2 illustrations how Elephant communicates with the animal kingdom every morning by displaying 5 coins, using his trunk to indicate where the sequence begins. As shown in Figure 3, Elephant asks Crow to display the first 3 coins and Rat to display the last two coins. When acting on behalf of Elephant, Crow and Rat each point to the first coin in their message, and the animal kingdom understands that Crow is to be read first. In this case Crow and Rat are not sending independent signals, but are instead following Elephant's instructions. On the other hand, if Crow and Rat are act independently, Crow controls 3 bits of entropy, while Rat controls 2 bits. The relationship between acting dependently and independently can be summarized as:

Elephants total, or net, entropy $S_{\text{Tot}}$ equals the sum of the entropies controlled by Crow and Rat, but the Template:Math number of messages Elephant can send equals the product of what Crow and Rat could send if they act independently:

Template:Spaces$S_{\text{Tot}}=S_{\text{Crow}}+S_{\text{Rat}}$ Template:Spaces $\iff$ Template:Spaces${\mathrm{\Omega }}_{\text{Tot}}={\mathrm{\Omega }}_{\text{Crow}}\cdot {\mathrm{\Omega }}_{\text{Rat}}$

Entropy is independent of the "alphabet" or "language" used

Neither our simple entropy $S$, nor the Shannon entropy $H$ do does not distinguish between the "language" or "alphabets" one might use when sending messages. Rat could equivalently send the messages by displaying two coins. Or messages could be expressed using binary numbers, or even four Arabic numbers using the four-sided die shown in Figure 3.

First derivation of Shannon entropy

$H=\underset{\text{all possible messages}}{\underbrace{\sum p_{j}lo{g}_2\left(p_j^{-1}\right)}}\equiv -\underset{\text{all possible messages}}{\underbrace{\sum p_{j}lo{g}_2\left(p_j\right)}}$

Expectation value reviewed

• w:Expected_value w:simple:Weighted average

The expectation, or "average" value of the four integers: $\{1,2,2,5\}$

$E(x)=\frac{1+2+2+5}{4}=2.5=\frac{1}{4}\cdot 1+\frac{1}{2}\cdot 2+\frac{1}{4}\cdot 5$

The fractions Template:Math,Template:Math, and Template:Math, refer to the probabilities of Template:Math being Template:Math, Template:Math, and Template:Math, respectively. This permits us to write the expectation value as a sum involving all probabilities:

$E(x)=1\cdot p_{(x=1)}+2\cdot p_{(x=2)}+5\cdot p_{(x=5)}\to \sum _x{p}_x\cdot x$

Additive property revisited

$-H_T=\sum _{k=1}^{N_T}{p}_k\log p_k,$ where $N_T=N_1{N}_2,$ and $p_k=p_{\alpha }{p}_{\beta },$

where the logarithm's base is two: $\log p_k\equiv {\log }_2(p_k).$

$-H_T=\sum _{i=1}^{N_1}\sum _{i=j}^{N_2}(p_i{p}_k)\log (p_i{p}_k)$ $=\sum _{i=1}^{N_1}\sum _{i=j}^{N_2}{p}_i{p}_k\cdot \underset{\log p_i{p}_j}{\underbrace{(\log p_i+\log p_k)}}$ $=\sum _{i=1}^{N_1}\sum _{i=j}^{N_2}(p_i{p}_j\log p_i+p_i{p}_j\log p_j)$ $=\underset{=1}{\underbrace{\left(\sum _{i=j}^{N_2}{p}_j\right)}}\sum _{i=1}^{N_1}{p}_i\log p_i+\underset{=1}{\underbrace{\left(\sum _{i=1}^{N_1}{p}_i\right)}}\sum _{j=1}^{N_2}{p}_j\log p_j$ $=\sum _{i=1}^{N_1}{p}_i\log p_i+\sum _{j=1}^{N_2}{p}_j\log p_j$ $=-H_1-H_2$

log2

$-H_T=\sum _{k=1}^{N_T}{p}_k{\log }_2{p}_k,$ where $N_T=N_1{N}_2,$ and $p_k=p_{\alpha }{p}_{\beta },$

where the logarithm's base is two: ${\log }_2{p}_k\equiv {\log }_2(p_k).$

$-H_T=\sum _{i=1}^{N_1}\sum _{i=j}^{N_2}(p_i{p}_k){\log }_2(p_i{p}_k)$ $=\sum _{i=1}^{N_1}\sum _{i=j}^{N_2}{p}_i{p}_k\cdot \underset{{\log }_2{p}_i{p}_j}{\underbrace{({\log }_2{p}_i+{\log }_2{p}_k)}}$ $=\sum _{i=1}^{N_1}\sum _{i=j}^{N_2}(p_i{p}_j{\log }_2{p}_i+p_i{p}_j{\log }_2{p}_j)$ $=\underset{=1}{\underbrace{\left(\sum _{i=j}^{N_2}{p}_j\right)}}\sum _{i=1}^{N_1}{p}_i{\log }_2{p}_i+\underset{=1}{\underbrace{\left(\sum _{i=1}^{N_1}{p}_i\right)}}\sum _{j=1}^{N_2}{p}_j{\log }_2{p}_j$ $=\sum _{i=1}^{N_1}{p}_i{\log }_2{p}_i+\sum _{j=1}^{N_2}{p}_j{\log }_2{p}_j$ $=-H_1-H_2$

Wheel of fortune

Shannon's entropy for unfair coin

$S_T=\log (n_C+n_R)$$=H_{CR}+\stackrel{p_C}{\overbrace{\frac{n_C}{n_C+n_R}}}\log n_C+\stackrel{p_R}{\overbrace{\frac{n_R}{n_C+n_R}}}\log n_R$

$H_{CR}=\log (n_C+n_R)-\stackrel{p_C}{\overbrace{\frac{n_C}{n_C+n_R}}}\log n_C-\stackrel{p_R}{\overbrace{\frac{n_R}{n_C+n_R}}}\log n_R$$=\log (n_C+n_R)-p_C\log n_C-p_R\log n_R$

Use fact that, $p_C+p_R=1,$ to write this as.

$H_{CR}$$=(p_C+p_R)\log (n_C+n_R)-p_C\log n_C-p_R\log n_R$ $=p_C\left(\underset{\log (1/p_C)}{\underbrace{\log (n_C+n_R)-\log n_C}}\right)-p_R\left(\underset{\log (1/p_R)}{\underbrace{\log (n_C+n_R)-\log n_R}}\right)$ $=p_{C}log(1/p_C)+p_{R}log(1/p_R)$

Another path to Shannon entropy

Move

Moved to Draft:Information theory/Permutations and combinations: $\text{If unlabeled: }\mathrm{\Omega }=5!=120\text{outcomes}$, $\text{If labeled: }\mathrm{\Omega }=\frac{(2+3)!}{2!3!}=10\text{outcomes}$

5 choose 3 versus permutation of ordered set of five objects.

Don't move

Employ fact that $\mathrm{\Omega }=2^S$ is often a very large number, since Template:Math is often a large number. A simplified version of Sterling's formula, $n!\approx n\ln n-n$ becomes for logarithms to base two:

$log(n!)\approx n\log n-\frac{n}{\ln 2}$ $log(n!)\approx n\log n-n/\ln 2$

$n=n_C+n_R$

$\tilde{S}=\log \left[\frac{(n_C+n_R)!}{n_C!n_R!}\right]$

$\approx (n_C+n_R)\log (n_C+n_R)-n_C\log n_C-n_R\log n_R$

$=n_C[\log (n_C+n_R)-\log n_C]+n_R[\log (n_C+n_R)-\log n_R]$

$\tilde{S}=n_C\log \left(\frac{n}{n_C}\right)+n_R\log \left(\frac{n}{n_R}\right)\text{if }n>>1$

table

Information entropy for collection of one-sided coins to simulate random events

Entropy per coin $(n_2=2n_1)$

$n_1+n_2$	Excel	Sterling
3	0.5283	0.5739
6	0.6511	0.6628
12	0.7459	0.7489
24	0.8120	0.8127
48	0.8549	0.8551
96	0.8814	0.8815
192	0.8973	0.8973
384	0.9065	0.9065
768	0.9117	0.9117
1536		0.9147
3072		0.9163
6144		0.9172
12288		0.9177
36864		0.9181
147456		0.9182
		0.9183

gamma from wikipedia

$n!=\mathrm{\Gamma }(n+1),$

$\sqrt{\pi }{\left(\frac{x}{e}\right)}^x{(8x^3+4x^2+x+\frac{1}{100})}^{1/6}<\mathrm{\Gamma }(1+x)<\sqrt{\pi }{\left(\frac{x}{e}\right)}^x{(8x^3+4x^2+x+\frac{1}{30})}^{1/6}.$

See also

• Permutation notation by user:Watchduck
• w:Permutation
• w:Combination
• w:Combinatorial proof
• w:Mathematical_proof
• b:Proof_by_Induction

EVERYTHING BELOW THIS IS SCRAPBOOK

Images used in this draft

• 
• 
• 
• 
• 
• 
• 
• 

Template:EquationRef: I hope I can use this here. There is no other page that might need it..

Two coin examples

$\begin{array}{ccccc}& TT& TH& HT& HH\\ H=& p_1{\log }_2(1/p_1)& +p_2{\log }_2(1/p_2)& +p_3{\log }_2(1/p_3)& +p_4{\log }_2(1/p_4)\\ 1=& 0& +0& +\frac{1}{2}{\log }_2(2)& +\frac{1}{2}{\log }_2(2)\\ 1.918...=& \frac{1}{3}\frac{1}{2}{\log }_2(6)& +\frac{1}{3}\frac{1}{2}{\log }_2(6)& +\frac{2}{3}\frac{1}{2}{\log }_2(3)& +\frac{2}{3}\frac{1}{2}{\log }_2(3)\\ 1.836...=& \frac{1}{3}\frac{1}{3}{\log }_2(9)& +\frac{1}{3}\frac{2}{3}{\log }_2(9/2)& +\frac{2}{3}\frac{1}{3}{\log }_2(9/2)& +\frac{2}{3}\frac{2}{3}{\log }_2(9/4)\end{array}$

additive property of shannon entropy

$-\mathrm{\Sigma }H=-(H_1+H_2)=\sum _{\alpha =1}^{N_1}{p}_{\alpha }\log p_{\alpha }+\sum _{\beta =1}^{N_2}{p}_{\beta }\log p_{\beta }.$

In our example, the crow's entropy is $H_1$, and $N_1=8$. The eight outcomes for the crow's three coins have probabilities:

$p_{\alpha }\in \{p_1,p_2,p_3,p_4,p_5,p_6,p_7,p_8\}$ for the outcomes $(000,001,010,011,100,101,111),$ respectively. Similarly, the set of Rat's four possible outcomes $p_{\beta }\in \{p_1,p_2,p_3,p_4\}$.

short

$-H_T=\sum _{k=1}^{N_T}{p}_k\log p_k,$ where $N_T=N_1{N}_2,$ and $p_k=p_{\alpha }{p}_{\beta }.$ $H_T=\sum _{i=1}^{N_1}\sum _{i=j}^{N_2}(p_i{p}_k)\log (p_i{p}_k)$ $=\sum _{i=1}^{N_1}\sum _{i=j}^{N_2}{p}_i{p}_k\cdot (\log p_i+\log p_k))$ $=\sum _{i=1}^{N_1}\sum _{i=j}^{N_2}(p_i{p}_j\log p_i+p_i{p}_j\log p_j)$ $=\sum _{i=j}^{N_2}{p}_j\sum _{i=1}^{N_1}{p}_i\log p_i+\sum _{i=1}^{N_1}{p}_i\sum _{j=1}^{N_2}{p}_j\log p_j$

Compression image

Students can explore image compression using Microsoft Paint. To a sequence of such images, copy an image into Microsoft Paint and successively reduce it's size by 50% N times. Then return each image back to its original size. In this example a coin from the jpeg Ephesos_620-600_BC.jpg was reduced a total of 6 times.

Image gallery

All images from the same randomized version of file:Image entropy with Inkscape First 01.svg

• 
  svg
• 
  png
• 
  svg × 4
• 
  png × 4

blurbs

I thought of calling it "information", but the word was overly used, so I decided to call it "uncertainty". [...] Von Neumann told me, "You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, nobody knows what entropy really is, so in a debate you will always have the advantage."

$\stackrel{{}^{\prime \prime }{1}^{\prime \prime }}{\overbrace{00}}\stackrel{{}^{\prime \prime }{2}^{\prime \prime }}{\overbrace{00}}\stackrel{{}^{\prime \prime }{3}^{\prime \prime }}{\overbrace{00}}\stackrel{{}^{\prime \prime }{4}^{\prime \prime }}{\overbrace{00}}$

Rules are needed to keep entropy "simple"

Crows messages are {000,001,010,011,100,101,111}, which corresponds to the integers 0-7 in base. The Crow could send more messages by choosing whether to include leading zeros, and the sole reason for forbidding such signals is to keep the system as simple as possible. For example, we "declare" the single sided coin to be incapable of conveying information because $log(1)=0$, and not because it is impossible to convey a message by not flipping a coin. Later, this convention that silence never conveys information will lead us to an alternative path to Shannon's formula for entropy.

H is Shannon entropy: H≤S

Shannon entropy $H$ is a generalization of the simple formula, of the simple formula, $S={\log }_2\mathrm{\Omega }$, that can be used to adjust for situations where some messages are either never sent, or are less likely to be sent. It involves the probability of certain messages be sent or not sent, and the formula can be used regardless of the mechanism responsible the messages are selected.

The vagueness associated with whether these probabilities are estimated by observation of many signals, or determined by some unknown means does not prevent Shannon's entropy from being useful. For example:

• Gadsby is a 50,000 word novel that does not contain the letter "e". Any casual analysis leads to the conclusion that the omission of the letter is deliberate.
• Those engaged in espionage can make inferences about a signal in which the "alphabet" appears to be a uniformly random sequence of letters can is likely to be encrypted.
• In written English, the letters "q" and "k" have the same pronunciation, which suggests that our text documents could be made smaller by removing the letter "q", for example, spelling "quick" as "quik". This is not much of a concern for text documents, but images and movies can be more easily stored or transmitted if compression is used.

The entropy of Rat's message does not depend on whether the binary system of two coins is used, or whether Rat displays the information using the four sided die shown in Figure 3.

Math

$\{HH,HT,TH,TT\}\iff \{00,01,10,11\}\iff \{\text{one},\text{two},\text{three},\text{four}\}$

 Letting, Template:Math = "heads" and Template:Math= "tails", these 4 outcomes can be described in a number of different ways.  Four such "outcomes" can also be counted in other ways, for example:

$\{HH,HT,TH,TT\}\iff \{00,01,10,11\}\iff \{\text{one},\text{two},\text{three},\text{four}\}$

This is the simplest example of the relationship between the

REWRITE: Figure 1 is currently being used by Wikipedias in five different languages. It illustrates the fact that the value of Shannon Entropy $S$ is the number of coins flipped:

, if the coins are “fair”, i.e. $S=N.$. The simplest example of an “unfair” coin would be one with either two “head” or two “tails”. Any reasonable measure of information content would ignore that coin and yield an entropy of $N-1.$ The scope of informal peek into the entropy is limited:

Figure 2:mThe elephant with 5 coins can send, $2^5=32,$ different messages, which is associated with 5 bits of information (if the coins are "fair"). If three coins are given the the crow and two coins to the rat, the crow can send, $2^3=8,$ different messages, while the rat can send only, $2^2=4,$ different messages. Even though the rat an crow can independently send only $8+4=12$ different messages, together, they possess the same number of bits of information, $2+3=5,$ as the elephant had. This illustrates the additive nature of entropy.

Assume all outcomes are equally probable

I find Crow the more illuminating, in part due to confusions 4=2×2 versus 4=2+2.  
it is often to count not coins but outcomes.  For rat equivalent to four sided coin.  The "alphabet" used to send information is not important.  Coins has advantage and disadvantage.  DELETE

$\underset{\text{equally probable}}{\underbrace{\stackrel{{}^{\prime \prime }{1}^{\prime \prime }}{\overbrace{00}}\stackrel{{}^{\prime \prime }{2}^{\prime \prime }}{\overbrace{00}}\stackrel{{}^{\prime \prime }{3}^{\prime \prime }}{\overbrace{00}}}}\underset{P}{\underbrace{\stackrel{{}^{\prime \prime }{4}^{\prime \prime }}{\overbrace{00}}}}$

$p_1=p_2=p_3=\frac{1-P}{3}⟹$

$p_1+p_2+p_3$

Appendix

Reminders

QB

• Information theory/Shannon entropy Reminders:
  • Include links from Information theory and Introduction_to_Information_Theory

---

decisions

1. REFERENCE Wikipedia Permalink section \#Characterization for two rigorous paths to Shannon's formula

Characterization

From w:Entropy (Information theory)

Let $\mathrm{I}$ be the information function which one assumes to be twice continuously differentiable, one has: $\begin{array}{cccccc}& \mathrm{I}(p_1{p}_2)& =& \mathrm{I}(p_1)+\mathrm{I}(p_2)& & \text{Starting from property 4}\\ & p_2{\mathrm{I}}^{\prime }(p_1{p}_2)& =& {\mathrm{I}}^{\prime }(p_1)& & \text{taking the derivative w.r.t}{p}_1\\ & {\mathrm{I}}^{\prime }(p_1{p}_2)+p_1{p}_2{\mathrm{I}}^{″}(p_1{p}_2)& =& 0& & \text{taking the derivative w.r.t}{p}_2\\ & {\mathrm{I}}^{\prime }(u)+u{\mathrm{I}}^{″}(u)& =& 0& & \text{introducing}u=p_1{p}_2\\ & (u\mapsto u{\mathrm{I}}^{\prime }(u){)}^{\prime }& =& 0\end{array}$ This differential equation leads to the solution $\mathrm{I}(u)=k\log u$ for any $k\in ℝ$. Property 2 leads to $k<0$. Properties 1 and 3 then hold also.

• What is the entropy S when one of the “unfair” in that the two outcomes occur with unequal probabilities.
• How can this definition be extended to include entities of more than two outcomes?
• What does it mean to say t

• hat entropy is an “extensive property”?
• How can this essay contribute to higher education?

Expected number of bits and entropy per symbol

w:Variable-length_code#Uniquely_decodable_codes helped me with w:Shannon's source coding theorem

Number of messages

This has a trivial resolution if we note that the exponential function, $y=lo{g}_2(x),$ and logarithmic function, $x=lo{g}_2(y),$ are mutually inverse functions:

$y=2^x\text{ if and only if }x={\log }_2(y)\dots (\text{ provided }y>0.)$

For example, the $\mathrm{\Omega }=6$ messages associated with the throw of a six-sided die has an entropy of $S=lo{g}_2(6)\approx 2.5585$

micro/macro state grand ensemble/Gibbs entropy

• These words are used differently and should be avoided
• w:Microstate (statistical mechanics)
• http://pillowlab.princeton.edu/teaching/statneuro2018/slides/notes08_infotheory.pdf uses Lagrangian multiplier to establish extremal See (8.19), or equivalently 8.2.2. See also efficiency at (8.22)

---

Since this essay is about the entropy of information,

large numbers

w:Observable_universe#Matter_content—number_of_atoms 10^80

1. no attempt to explain. This introduction the formula is not rigorous. purpose familiarize properties. slowly build, begin w info result of randon generator flipping N coins, ignoring surpisal. N evolves to shannon entropy.
2. The elephant shown to right uses 5 coins to send messages. Sometimes he gives three coins to the crow and two coins to the rat so they can also send messages. The number of possible messages available to each animal depends on how many coins are used.

1. kilobytes is a smallfile
   1. https://en.wikipedia.org/wiki/Byte
   2. https://en.wikipedia.org/wiki/Kilobyte

Links

• b:An Intuitive Guide to the Concept of Entropy Arising in Various Sectors of Science Uses Stirling approximation to show the p log p arises from large amounts of entropy.
• towardsdatascience.com pages can be accessed for free at first, but later it seems you need to pay.
• https://planetcalc.com/2476/
• w:Stirling's approximation
• https://math.stackexchange.com/questions/331103/intuitive-explanation-of-entropy
• https://en.wikipedia.org/w/index.php?title=Entropy_in_thermodynamics_and_information_theory&oldid=1020584746#See_also
  • Interesting links, mostly to WP
• https://en.wikipedia.org/w/index.php?title=Entropy_(information_theory)&oldid=1033726547#Characterization
  • 2 derivations of PlogP stuff.
  • I=-log p is information content (low p means big I)
  • already referenced!
• https://en.wikipedia.org/wiki/Entropy_(statistical_thermodynamics)
  • Uses log n! = n log n to justify PlogP stuff
• w:Binary entropy function graphs $\mathrm{H}(X)={\mathrm{H}}_{\text{b}}(p)=-p{\log }_{2}p-(1-p){\log }_2(1-p)$,

Boltzmann or Gibbs?

• w:Boltzmann's entropy formula