Draft:Linear algebra/Introduction

Linear algebra

Linear algebra is a branch of mathematics that studies objects called vectors, vector spaces, linear equations, linear maps, and matrices. It also studies how these objects all interact with each other.

Vectors

Error creating thumbnail:

An example of a vector in 'arrow form'

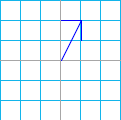
A vector is a way to represent co-ordinates. The top number is its x coordinate, the number below that is the y coordinate, then the z co-ordinate, and so on, until the vector stops. $(\genfrac{}{}{0ex}{}{1}{2})$, for example, is a point in which, if you start at the origin, then walk one step to the right (to the right because it's positive), then two steps forward (forward because it's positive), you will get there. There is also another representation, which is an arrow from the origin (the point in which the red lines intersect, or $(\genfrac{}{}{0ex}{}{0}{0})$) to the point that is mentioned. For the rest of this, the arrow will be used.

Basis vectors

The basis vectors are a set of vectors that every other vector is written as a sum of. There are a set of basis vectors, depending on the dimension you're working with.

1d case

In the 1d case, the basis vector is the one with the x-coordinate set as 1 (i.e. (1); termed 'i hat'). Everything else, like (-5) can be written as -5(1)

2d case

In the 2d case, there are two basis vectors, i hat and j hat, written as $(\genfrac{}{}{0ex}{}{1}{0})$ and $(\genfrac{}{}{0ex}{}{0}{1})$, respectively. Again, everything else, like $(\genfrac{}{}{0ex}{}{3}{2})$ can be written as $3(\genfrac{}{}{0ex}{}{1}{0})+2(\genfrac{}{}{0ex}{}{0}{1})$.

3d case

In the 3d case, there are three basis vectors, i hat, j hat and k hat, written as $\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$, $\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)$ and $\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$, respectively. As with the other two cases, everything else, like $\left(\begin{array}{c}3\\ 4\\ 5\end{array}\right)$ can be written as $3\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)+4\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)+5\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$.

Higher dimensional cases

There is an obvious pattern here. Any n-dimensional vector requires n basis vectors. Similarly, the basis vectors have a one in one of the entries and 0's on all of the others.

Matrices

A matrix is a thing that turns vectors into other vectors. Lets use an example, like $\left(\begin{array}{cc}1& 2\\ 3& 4\end{array}\right)$. $\left(\begin{array}{cc}1& 2\\ 3& 4\end{array}\right)$ means that i-hat (that's $\left(\begin{array}{c}1\\ 0\end{array}\right)$, in case you weren't paying attention) turns into $\left(\begin{array}{c}1\\ 3\end{array}\right)$ and j-hat (that's $\left(\begin{array}{c}0\\ 1\end{array}\right)$ btw) turns into $\left(\begin{array}{c}2\\ 4\end{array}\right)$. Now, let's say that we want to create a vector changing machine using that matrix. Well, that leads us to the next subsection!

Matrix-Vector multiplication

Say we want to put a vector, say $\left(\begin{array}{c}5\\ 6\end{array}\right)$ into our vector changing machine (a matrix). We write it like this: $\left(\begin{array}{cc}1& 2\\ 3& 4\end{array}\right)\left(\begin{array}{c}5\\ 6\end{array}\right)$. Now what would the machine actually do? Well, let's think about it. Well, recall that my matrix means that i-hat turns into $\left(\begin{array}{c}1\\ 3\end{array}\right)$ and j-hat turns into $\left(\begin{array}{c}2\\ 4\end{array}\right)$. Now $\left(\begin{array}{c}5\\ 6\end{array}\right)$ means 5*i-hat+6*j-hat. We can just replace i-hat and j-hat into what they turn into! So $\left(\begin{array}{cc}1& 2\\ 3& 4\end{array}\right)\left(\begin{array}{c}5\\ 6\end{array}\right)=5\left(\begin{array}{c}1\\ 3\end{array}\right)+6\left(\begin{array}{c}2\\ 4\end{array}\right)$. Now notice that $5\left(\begin{array}{c}1\\ 3\end{array}\right)=\left(\begin{array}{c}5\\ 15\end{array}\right)$ and $6\left(\begin{array}{c}2\\ 4\end{array}\right)=\left(\begin{array}{c}12\\ 24\end{array}\right)$. Now when we add them up, we get: $\left(\begin{array}{c}17\\ 39\end{array}\right)$. And there's our answer!

Matrix Multiplication

But I want to make a matrix out of spare parts! Well, here's how!