Draft:Original research/MacLaurin series

This graph show the use of a MacLaurin series to approximate the sine of x, or sin(x), when x = 0, and other values determined by polynomials with degree Template:Font, Template:Font, Template:Font, Template:Font, Template:Font, Template:Font and Template:Font. Credit: IkamusumeFan.

A MacLaurin series is a Taylor series that has a term at (0,0).

A Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point. Template:Clear

Calculuses

This diagram shows an approximation to an area under a curve. Credit: Dubhe.

Notation: let the symbol $\mathrm{\Delta }$ represent difference in a variable.

Notation: let the symbol $d$ represent an infinitesimal difference in a variable.

Notation: let the symbol $\partial$ represent an infinitesimal difference in one input to a function of more than one input.

Let

$y=f(x)$

be a function where values of $x$ may be any real number and values resulting in $y$ are also any real number.

$\mathrm{\Delta }x$ is a small finite difference in $x$ which when put into the function $f(x)$ produces a $\mathrm{\Delta }y$.

These small differences can be manipulated with the operations of arithmetic: addition ($+$), subtraction ($-$), multiplication ($*$), and division ($/$).

$\mathrm{\Delta }y=f(x+\mathrm{\Delta }x)-f(x)$

Dividing $\mathrm{\Delta }y$ by $\mathrm{\Delta }x$ and taking the limit as $\mathrm{\Delta }x$ → 0, produces the slope of a line tangent to f(x) at the point x.

For example,

$f(x)=x^2$

$f(x+\mathrm{\Delta }x)=(x+\mathrm{\Delta }x{)}^2=x^2+2x\mathrm{\Delta }x+(\mathrm{\Delta }x{)}^2$

$\mathrm{\Delta }y/\mathrm{\Delta }x=(x^2+2x\mathrm{\Delta }x+(\mathrm{\Delta }x{)}^2-x^2)/\mathrm{\Delta }x$

$\mathrm{\Delta }y/\mathrm{\Delta }x=2x+\mathrm{\Delta }x$

as $\mathrm{\Delta }x$ and$\mathrm{\Delta }y$ go towards zero,

$dy/dx=2x+dx=limi{t}_{\mathrm{\Delta }x\to 0}\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}=2x.$

This ratio is called the derivative.

Let

$y=f(x,z)$

then

$\partial y=\partial f(x,z)=\partial f(x,z)\partial x+\partial f(x,z)\partial z$

$\partial y/\partial x=\partial f(x,z)$

where z is held constant and

$\partial y/\partial z=\partial f(x,z)$

where x is held contstant.

Notation: let the symbol $\mathrm{\nabla }$ be the gradient, i.e., derivatives for multivariable functions.

$\mathrm{\nabla }f(x,z)=\partial y=\partial f(x,z)=\partial f(x,z)\partial x+\partial f(x,z)\partial z.$

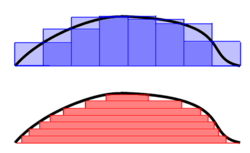
For

$\mathrm{\Delta }x*\mathrm{\Delta }y=[f(x+\mathrm{\Delta }x)-f(x)]*\mathrm{\Delta }x$

the area under the curve shown in the diagram at right is the light purple rectangle plus the dark purple rectangle in the top figure

$\mathrm{\Delta }x*\mathrm{\Delta }y+f(x)*\mathrm{\Delta }x=f(x+\mathrm{\Delta }x)*\mathrm{\Delta }x.$

Any particular individual rectangle for a sum of rectangular areas is

$f(x_i+\mathrm{\Delta }{x}_i)*\mathrm{\Delta }{x}_i.$

The approximate area under the curve is the sum $\sum$ of all the individual (i) areas from i = 0 to as many as the area needed (n):

$\sum _{i=0}^{n}f(x_i+\mathrm{\Delta }{x}_i)*\mathrm{\Delta }{x}_i.$

Notation: let the symbol $\int$ represent the integral.

$limi{t}_{\mathrm{\Delta }x\to 0}\sum _{i=0}^{n}f(x_i+\mathrm{\Delta }{x}_i)*\mathrm{\Delta }{x}_i=\int f(x)dx.$

This can be within a finite interval [a,b]

$\underset{a}{\overset{b}{\int }}f(x)dx$

when i = 0 the integral is evaluated at $a$ and i = n the integral is evaluated at $b$. Or, an indefinite integral (without notation on the integral symbol) as n goes to infinity and i = 0 is the integral evaluated at x = 0.

Def. a branch of mathematics that deals with the finding and properties ... of infinitesimal differences is called a calculus.

Calculus focuses on limits, functions, derivatives, integrals, and infinite series.

"Although calculus (in the sense of analysis) is usually synonymous with infinitesimal calculus, not all historical formulations have relied on infinitesimals (infinitely small numbers that are nevertheless not zero)."

Series

Template:Main Taylor Series:

$y=\sum _{n=0}^{\mathrm{\infty }}\frac{f^n(a)(x-a{)}^n}{n!}=f(a)+f^{\prime }(a)(x-a)+\frac{f^{″}(a)(x-a{)}^2)}{2!}+\frac{f^{‴}(a)(x-a{)}^3}{3!}+...,$

where fⁿ refers to the number (n) of derivatives taken.

A MacLaurin series of a function ƒ(x) for which a derivative may be taken of the function or any of its derivatives at 0 is the power series

$f(0)+\frac{f^{\prime }(0)}{1!}(x)+\frac{f^{″}(0)}{2!}(x{)}^2+\frac{f^{(3)}(0)}{3!}(x{)}^3+\cdots .$

which can be written in the more compact sigma, or summation, notation as

$\sum _{n=0}^{\mathrm{\infty }}\frac{f^{(n)}(0)}{n!}(x{)}^n$

where n! denotes the factorial of n and ƒ ⁽ⁿ⁾(0) denotes the nth derivative of ƒ evaluated at the point 0. The derivative of order zero ƒ is defined to be ƒ itself and Template:Nowrap and 0! are both defined to be 1.

MacLaurin series for e^x

Taylor series is defined as

$\sum _{n=0}^{\mathrm{\infty }}\frac{f^{(n)}(t)}{n!}(x-t{)}^n$

The MacLaurin series occurs when t=0

$\sum _{n=0}^{\mathrm{\infty }}\frac{f^{(n)}(0)}{n!}(x{)}^n$

The derivatives are

$y\text{'}=e^x$

$y{\text{'}}^{\prime }=e^x$

$y{\text{'}}^{″}=e^x$

.

.

.

Development of MacLaurin series for $e^x$

$e^x=\frac{1}{0!}+\frac{1}{1!}x+\frac{1}{2!}{x}^2+\frac{1}{3!}{x}^3\dots$

$e^x=1+x+\frac{1}{2}{x}^2+\frac{1}{6}{x}^3\dots$

Explicit form can be written as

$e^x=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}(x{)}^n$

MacLaurin series for the natural logarithm

The natural logarithm (with base Template:Mvar) has Maclaurin series

$\begin{array}{cc}\log (1-x)& =-\sum _{n=1}^{\mathrm{\infty }}\frac{x^n}{n}=-x-\frac{x^2}{2}-\frac{x^3}{3}-\cdots ,\\ \log (1+x)& =\sum _{n=1}^{\mathrm{\infty }}(-1{)}^{n+1}\frac{x^n}{n}=x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots .\end{array}$

They converge for $|x|<1$.

MacLaurin series for sin(x)

$y=sin(t)$

$y^{\prime }=cos(t)$

$y^{″}=-sin(t)$

$y^{‴}=-cos(t)$

$y^{iv}=sin(t)$

$y^v=cos(t)$

.

.

.

Development of MacLaurin series for $sin(x)$

$sin(x)=\frac{0}{0!}+\frac{1}{1!}x-\frac{0}{2!}{x}^2-\frac{1}{3!}{x}^3+\frac{0}{4!}{x}^4+\frac{1}{5!}{x}^5...$

$sin(x)=1x-\frac{1}{6}{x}^3+\frac{1}{120}{x}^5...$

Explicit form can be written as

$sin(x)=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n+1)!}(x{)}^{(2n+1)}$

MacLaurin series for cos(x)

Development of MacLaurin series for $cos(x)$

$y=cos(t)$

$y^{\prime }=-sin(t)$

$y^{″}=-cos(t)$

$y^{‴}=sin(t)$

$y^{iv}=cos(t)$

.

.

.

$cos(x)=\frac{1}{0!}+\frac{0}{1!}x-\frac{1}{2!}{x}^2+\frac{0}{3!}{x}^3+\frac{1}{4!}{x}^4\dots$

$cos(x)=1-\frac{1}{2}{x}^2+\frac{1}{24}{x}^4...$

Explicit form can be written as

$cos(x)=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n)!}(x{)}^{2n}$

Euler's formula

Recalling Euler's Formula:

$e^{i\omega x}=\cos \omega x+i\sin \omega x$

Recall the Taylor Series from above for $e^x$ at :$t=0$ (also called the MacLaurin series)

$e^x=\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}$

By replacing x with $i\omega x$, the Taylor series for $e^{i\omega x}$ can be found:

$e^{i\omega x}=\sum _{n=0}^{\mathrm{\infty }}\frac{(i\omega x{)}^n}{n!}$

even powers of n = 2k:

$i^{2k}=(i^2{)}^k=(-1{)}^k$

odd powers of n = 2k+1:

$i^{2k+1}=(i^2{)}^{k}i=(-1{)}^{k}i$

For $i\omega x$:

$e^{i\omega x}=\sum _{n=0}^{\mathrm{\infty }}\frac{i^n(\omega x{)}^n}{n!}=\sum _{k=0}^{\mathrm{\infty }}\frac{i^{2k}(\omega x{)}^{2k}}{(2k)!}+\sum _{k=0}^{\mathrm{\infty }}\frac{i^{2k+1}(\omega x{)}^{2k+1}}{(2k+1)!}$

Using the two previous equations:

$e^{i\omega x}=\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k(\omega x{)}^{2k}}{(2k)!}+i\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k(\omega x{)}^{2k+1}}{(2k+1)!}$

$\Rightarrow e^{i\omega x}=\cos (\omega x)+i\sin (\omega x)$

Therefore, the first part of the equation is equal to the Taylor series for cosine, and the second part is equal to the Taylor series for sine as follows:

$\cos (\omega x)=\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k(\omega x{)}^{2k}}{(2k)!}$

$\sin (\omega x)=\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k(\omega x{)}^{2k+1}}{(2k+1)!}$

MacLaurin series for $(1-x{)}^{-a}$

$f(x)=\frac{1}{(1-x{)}^a}$

Template:Center topTable for Maclaurin SeriesTemplate:Center bottom
$f(x)=\frac{1}{(1-x{)}^a}$	$f(0)=\frac{1}{(1-0{)}^a}=1$
$f^{\prime }(x)=\frac{a}{(1-x{)}^{a+1}}$	$f^{\prime }(0)=\frac{a}{(1-0{)}^{a+1}}=a$
$f^{″}(x)=\frac{a(a+1)}{(1-x{)}^{a+2}}$	$f^{″}(0)=\frac{a(a+1)}{(1-0{)}^{a+2}}=a(a+1)$
$f^{(3)}(x)=\frac{a(a+1)(a+2)}{(1-x{)}^{a+3}}$	$f^{(3)}(0)=\frac{a(a+1)(a+2)}{(1-0{)}^{a+3}}=a(a+1)(a+2)$
And so on..	..

Rewriting the Maclaurin series expansion,

$\frac{1}{(1-x{)}^a}=f(0)+\frac{f^{\prime }(0)}{1!}(x-0)+\frac{f^{″}(0)}{2!}(x-0{)}^2+\frac{f^{(3)}(0)}{3!}(x-0{)}^3+\cdots .$

Substituting the values from the table, we get

$\frac{1}{(1-x{)}^a}=1+\frac{a}{1!}(x)+\frac{a(a+1)}{2!}(x{)}^2+\frac{a(a+1)(a+2)}{3!}(x{)}^3+\cdots .$

$\frac{1}{(1-x{)}^a}=\sum _{n=0}^{\mathrm{\infty }}(a{)}_k\frac{x^k}{n!}$

Using

$(a{)}_0:=1$

$(a{)}_k:=a(a+1)(a+2)\cdots (a+k-1)$

We can represent

$\sum _{n=0}^{\mathrm{\infty }}\frac{(a{)}_k(b{)}_k}{(c{)}_k}\frac{x^k}{n!}=F(a,b;c;x)$

$\sum _{n=0}^{\mathrm{\infty }}\frac{(a{)}_k(b{)}_k}{(b{)}_k}\frac{x^k}{n!}=F(a,b;b;x)$

Binomial series

The binomial series is the power series

$(1+x{)}^{\alpha }=\sum _{n=0}^{\mathrm{\infty }}(\genfrac{}{}{0ex}{}{\alpha }{n})x^n$

whose coefficients are the generalized binomial coefficients

$(\genfrac{}{}{0ex}{}{\alpha }{n})=\prod _{k=1}^n\frac{\alpha -k+1}{k}=\frac{\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}.$

(If Template:Math, this product is an empty product and has value 1.) It converges for $|x|<1$ for any real or complex number Template:Mvar.

When Template:Math, this is essentially the infinite geometric series mentioned in the previous section. The special cases Template:Math and Template:Math give the square root function and its inverse:

$\begin{array}{cc}(1+x{)}^{\frac{1}{2}}& =1+\frac{1}{2}x-\frac{1}{8}{x}^2+\frac{1}{16}{x}^3-\frac{5}{128}{x}^4+\frac{7}{256}{x}^5-\dots ,\\ (1+x{)}^{-\frac{1}{2}}& =1-\frac{1}{2}x+\frac{3}{8}{x}^2-\frac{5}{16}{x}^3+\frac{35}{128}{x}^4-\frac{63}{256}{x}^5+\dots .\end{array}$

When only the linear term is retained, this simplifies to the binomial approximation.

MacLaurin series for $arctan(1+x)$

We have the function

$arctan(1+x)$

Expand $arctan(1+x)$

Template:Center topTable for Maclaurin SeriesTemplate:Center bottom
$f(x)=arctan(1+x)$	$f(0)=arctan(1+0)=\frac{\pi }{4}$
$f^{\prime }(x)=\frac{1}{1+(1+x{)}^2}$	$f^{\prime }(0)=\frac{1}{1+(1+0{)}^2}=\frac{1}{2}$
$f^{″}(x)=\frac{-2(x+1)}{{[1+(1+x{)}^2]}^2}$	$f^{″}(0)=\frac{-2(0+1)}{{[1+(1+0{)}^2]}^2}=\frac{-1}{2}$
$f^{(3)}(x)=\frac{2(3x^2+6x+2)}{{[1+(1+x{)}^2]}^3}$	$f^{(3)}(0)=\frac{2(3(0{)}^2+6(0)+2)}{{[1+(1+0{)}^2]}^3}=\frac{1}{2}$
And so on..	..

Rewriting the Maclaurin series expansion,

$arctan(1+x)=f(0)+\frac{f^{\prime }(0)}{1!}(x-0)+\frac{f^{″}(0)}{2!}(x-0{)}^2+\frac{f^{(3)}(0)}{3!}(x-0{)}^3+\cdots .$

Substituting the values from the table, we get

$arctan(1+x)=\frac{\pi }{4}+\frac{1}{2*1!}(x)-\frac{1}{2*2!}(x{)}^2+\frac{1}{2*3!}(x{)}^3+\cdots .$

MacLaurin series for $arctan(x)$

$arctan(x)$

Expanding $arctan(x)$ using Maclaurin's series

Template:Center topTable for Maclaurin SeriesTemplate:Center bottom
$f(x)=arctan(x)$	$f(0)=arctan(0)=0$
$f^{\prime }(x)=\frac{1}{1+x^2}$	$f^{\prime }(0)=\frac{1}{1+(0{)}^2}=1$
$f^{″}(x)=\frac{-2x}{{[1+x^2]}^2}$	$f^{″}(0)=\frac{-2(0)}{{[1+(0{)}^2]}^2}=0$
$f^{(3)}(x)=\frac{6x^2-2}{{[1+x^2]}^3}$	$f^{(3)}(0)=\frac{6(0{)}^2-2}{{[1+(0{)}^2]}^3}=-2$
$f^{(4)}(x)=\frac{-24x(x^2-1)}{{[1+x^2]}^4}$	$f^{(4)}(0)=\frac{-24(0)((0{)}^2-1)}{{[1+(0{)}^2]}^4}=0$
$f^{(5)}(x)=\frac{24(5x^4-10x^2+1)}{{[1+x^2]}^5}$	$f^{(5)}(x)=\frac{24(5(0{)}^4-10(0{)}^2+1)}{{[1+(0{)}^2]}^5}=24$
And so on..	..

Rewriting the Maclaurin series expansion,

$arctan(x)=f(0)+\frac{f^{\prime }(0)}{1!}(x-0)+\frac{f^{″}(0)}{2!}(x-0{)}^2+\frac{f^{(3)}(0)}{3!}(x-0{)}^3+\cdots .$

Substituting the values from the table, we get

$arctan(x)=0+\frac{1}{1!}(x)+\frac{0}{2!}(x{)}^2+\frac{-2}{3!}(x{)}^3+\frac{0}{4!}(x{)}^4+\frac{24}{5!}(x{)}^5\cdots .$

MacLaurin series for trigonometric functions

$\begin{array}{cccccc}\sin x& =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}& & =x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots & & \text{for all }x\\ \cos x& =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n)!}{x}^{2n}& & =1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots & & \text{for all }x\\ \tan x& =\sum _{n=1}^{\mathrm{\infty }}\frac{B_{2n}(-4{)}^n(1-4^n)}{(2n)!}{x}^{2n-1}& & =x+\frac{x^3}{3}+\frac{2x^5}{15}+\cdots & & \text{for }|x|<\frac{\pi }{2}\\ \sec x& =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n{E}_{2n}}{(2n)!}{x}^{2n}& & =1+\frac{x^2}{2}+\frac{5x^4}{24}+\cdots & & \text{for }|x|<\frac{\pi }{2}\\ \arcsin x& =\sum _{n=0}^{\mathrm{\infty }}\frac{(2n)!}{4^n(n!{)}^2(2n+1)}{x}^{2n+1}& & =x+\frac{x^3}{6}+\frac{3x^5}{40}+\cdots & & \text{for }|x|\le 1\\ \arccos x& =\frac{\pi }{2}-\arcsin x\\ & =\frac{\pi }{2}-\sum _{n=0}^{\mathrm{\infty }}\frac{(2n)!}{4^n(n!{)}^2(2n+1)}{x}^{2n+1}& & =\frac{\pi }{2}-x-\frac{x^3}{6}-\frac{3x^5}{40}-\cdots & & \text{for }|x|\le 1\\ \arctan x& =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{2n+1}{x}^{2n+1}& & =x-\frac{x^3}{3}+\frac{x^5}{5}-\cdots & & \text{for }|x|\le 1,x\ne \pm i\end{array}$

All angles are expressed in radians. The numbers Template:Math appearing in the expansions of Template:Math are the Bernoulli numbers. The Template:Math in the expansion of Template:Math are Euler numbers.

Engineering

Template:Main The "performance of a Markov system under different operating strategies [can be estimated] by observing the behavior of the system under the [strategy of having] a Maclaurin series for the performance measures of [the] Markov chains."

Hypotheses

1. Any non-convergent function can be represented by a MacLaurin series.

See also

• MacLaurin series (18 kB) (3 February 2020)
• Mathematics (41 kB) (17 September 2019)
• Solution for sin(t)
• Solutions to problem set 2.7

External links

• African Journals Online
• Bing Advanced search
• Google Books
• Google scholar Advanced Scholar Search
• International Astronomical Union
• JSTOR
• Lycos search
• NASA/IPAC Extragalactic Database - NED
• NASA's National Space Science Data Center
• NCBI All Databases Search
• Office of Scientific & Technical Information
• Questia - The Online Library of Books and Journals
• SAGE journals online
• The SAO/NASA Astrophysics Data System
• Scirus for scientific information only advanced search
• SDSS Quick Look tool: SkyServer
• SIMBAD Astronomical Database
• SIMBAD Web interface, Harvard alternate
• Spacecraft Query at NASA
• SpringerLink
• Taylor & Francis Online
• Universal coordinate converter
• Wiley Online Library Advanced Search
• Yahoo Advanced Web Search