Inversion (discrete mathematics)

A permutation, its inversion set and its left inversion count

Inversion is a concept in discrete mathematics to measure how much a sequence is out of its natural order.

(An inversion of a permutation is not to be confused with the inverse of a permutation. Also not with point reflection.)

Definitions

Map from the place-based to the element-based inversions of a permutation of four elements

The element-based inversion multiset of this sequence contains (2,1) twice.

A permutation $\pi$ has an inversion for each pair of elements that are out of their natural order, i.e. when $i<j$ but $\pi (i)>\pi (j)$.
It may be identified by the pair of places $(i,j)$ or by the pair of elements $(\pi (i),\pi (j))$.
This article favours the former convention (although the latter seems to be more common).

The inversion set of a permutation is the set of all its inversions.
For an $n$-element permutation the number of potential elements is the triangular number $(\genfrac{}{}{0ex}{}{n}{2})$.

The element-based inversion set is essentially the place-based inversion set of the inverse permutation, just with the elements of the pairs exchanged.

For sequences the element-based inversion set has to be defined as a multiset, as many pairs of places can have the same pair of elements.

The permutation graph has the elements of the permutation as vertices and an edge between elements that are out of order,
i.e. an edge is an inversion according to the element-based definition: $\{\pi (i),\pi (j)\}$ is an edge iff $i<j\wedge \pi (i)>\pi (j)$.
It is more common to write that $\{i,j\}$ is an edge iff $i<j\wedge {\pi }^{-1}(i)>{\pi }^{-1}(j)$. The latter is often written as $(i-j)\cdot ({\pi }^{-1}(i)-{\pi }^{-1}(j))<0$.

The permutation graphs of inverse permutations are isomorphic. That of ${\pi }^{-1}$ can be generated from that of $\pi$ by changing each vertex $i$ to $\pi (i)$.

It seems that the permutation graph is only defined with place-based inversions. If it were generalized to apply to sequences, it would thus have to be defined as a multigraph.

The inversion number (Template:Oeis) is the cardinality of the inversion set;
thus also the digit sum of the inversion related vectors;
and also the number of crossings in the arrow diagram of the permutation.

The parity of a permutation is the parity of its inversion number.
The sign of a permutation (the determinant of its matrix) corresponds to the parity: Even permutations have sign 1, odd permutations sign −1.

Inversion related vectors

There are four ways to condense the inversions of a permutation into a vector that uniquely determines it. Three of them are in use. (See sources below).

This article uses the terms left inversion count (Template:Invvect) and right inversion count (Template:Invvect) like Gnedin (similar to Calude and Deutsch), and the term inversion vector (Template:Invvect) like Wolfram.

The left and right inversion counts have the feature that interpreted as factorial numbers they determine the permutation's reverse colexicographic and lexicographic index.
The inversion vector does not appear to have a similar advantage, but it is widely used anyway.

Left inversion count Template:Invvect:
With the place-based definition $l(i)$ is the number of inversions whose bigger (right) component is $i$.

$l(i)$ is the number of elements in $\pi$ greater than $\pi (i)$ before $\pi (i)$.

$l(i)=\mathrm{\#}\{k\mid k<i\wedge \pi (k)>\pi (i)\}$

Right inversion count Template:Invvect, often called Template:W:
With the place-based definition $r(i)$ is the number of inversions whose smaller (left) component is $i$.

$r(i)$ is the number of elements in $\pi$ smaller than $\pi (i)$ after $\pi (i)$.

$r(i)=\mathrm{\#}\{k\mid k>i\wedge \pi (k)<\pi (i)\}$

Inversion vector Template:Invvect:
With the element-based definition $v(i)$ is the number of inversions whose smaller (right) component is $i$.

$v(i)$ is the number of elements in $\pi$ greater than $i$ before $i$.

$v(i)=\mathrm{\#}\{k\mid k>i\wedge {\pi }^{-1}(k)<{\pi }^{-1}(i)\}$

A different way to say the same thing may be more intuitive:

$v(\pi (i))$ is the number of elements in $\pi$ greater than $\pi (i)$ before $\pi (i)$.

$v(\pi (i))=\mathrm{\#}\{k\mid k<i\wedge \pi (k)>\pi (i)\}=l(i)$

The latter definition would also work for a sequence, which does not have an inverse.

Python functions
def left_inversion_count(p): n = len(p) v = [0] * n for i in range(n): count = 0 for k in range(i): if p[k] > p[i]: count += 1 v[i] = count return v	def right_inversion_count(p): n = len(p) v = [0] * n for i in range(n): count = 0 for k in range(i, n): if p[k] < p[i]: count += 1 v[i] = count return v	def inversion_vector(p_raw): if min(p_raw) == 1: # assuming 1-based permutation p = [entry-1 for entry in p_raw] else: # assuming 0-based permutation p = p_raw n = len(p) v = [0] * n for i in range(n): count = 0 for k in range(i): if p[k] > p[i]: count += 1 v[p[i]] = count return v

Relationship between Template:Invvect and Template:Invvect:

$v=l.\pi =l({\pi }^{-1})$	$\iff$	$v(i)=l({\pi }^{-1}(i))$	(vector $x$ permuted by $\alpha$ is $x.\alpha =x({\alpha }^{-1})$, compare Permutation notation)
$l=v.{\pi }^{-1}=v(\pi )$	$\iff$	$l(i)=v(\pi (i))$

The first digit of Template:Invvect and the last digit of Template:Invvect are always 0, and can be omitted.
When these vectors are permuted into each other, the omissible 0 from one does not necessarily become the omissible 0 in the other.

Relationship between Template:Invvect and Template:Invvect:
Both Template:Invvect and Template:Invvect can be found with the help of a Rothe diagram,
which is a permutation matrix with the 1s represented by dots, and an inversion in every position that has a dot to the right and below it.
$r(i)$ is the sum of inversions in row $i$ of the Rothe diagram, while $v(i)$ is the sum of inversions in column $i$.
The permutation matrix of the inverse is the transpose. Therefore Template:Invvect of a permutation is Template:Invvect of its inverse, and vice versa.

Relationship between Template:Invvect and Template:Invvect:

$\pi (i)=i+r(i)-l(i)$

This is proven in Gnedin & Olshanski 2012, and mentioned as R[i]+i=p[i]+L[i] in Template:Oeis.

Permutations that are equal up to fixed points can be seen as equal. Equivalently, inversion related vectors that are equal up to trailing 0s can be seen as equal.
While for Template:Invvect and Template:Invvect the omissible 0 on the right is part of the trailing 0s, for Template:Invvect the omissible 0 on the left is separate from them.

Example: Permutations of six elements

The following images show two inverse permutations, their 9 inversions and the corresponding vectors.

$v=l.\pi =l({\pi }^{-1})$ $v(3)=l({\pi }^{-1}(3))=l(5)=3$ $l=v.{\pi }^{-1}=v(\pi )$ $l(3)=v(\pi (3))=v(4)=1$

$\begin{array}{cc}\pi & =674\\ & =(125346)\\ & =\left(\begin{array}{cccccc}1& 2& 3& 4& 5& 6\\ 2& 5& 4& 6& 3& 1\end{array}\right)\end{array}$ Permutation matrix

Rothe diagram

Place-based inversion set Template:Invvect = (0, 0, 1, 0, 3, 5) rev colex rank: 530100! = 674 Template:Invvect = (1, 3, 2, 2, 1, 0) lex rank: 132210! = 209

Element-based inversion set Permutation graph

$v=l.\pi =l({\pi }^{-1})$ $v(3)=l({\pi }^{-1}(3))=l(4)=2$ $l=v.{\pi }^{-1}=v(\pi )$ $l(3)=v(\pi (3))=v(5)=1$

$\begin{array}{cc}\pi & =327\\ & =(164352)\\ & =\left(\begin{array}{cccccc}1& 2& 3& 4& 5& 6\\ 6& 1& 5& 3& 2& 4\end{array}\right)\end{array}$ Permutation matrix

Rothe diagram

File:Inversion example; invset p-b 2.svg Place-based inversion set Template:Invvect = (0, 1, 1, 2, 3, 2) rev colex rank: 232110! = 327 Template:Invvect = (5, 0, 3, 1, 0, 0) lex rank: 503100! = 620

Error creating thumbnail: Element-based inversion set Permutation graph

Mathematica omits the 0 at the end of the inversion vector. Compare p1 and p2 in Wolfram Alpha.

I: p1 = {2,5,4,6,3,1}
I: p2 = {6,1,5,3,2,4}

I: ToInversionVector[p1]
O: {5,0,3,1,0}
I: ToInversionVector[p2]
O: {1,3,2,2,1}

I: ToOrderedPairs[PermutationGraph[p1]]
O: {{2,1},{3,1},{4,1},{5,1},{6,1},{4,3},{5,3},{6,3},{5,4},{1,2},{1,3},{1,4},{1,5},{1,6},{3,4},{3,5},{3,6},{4,5}}
I: ToOrderedPairs[PermutationGraph[p2]]
O: {{6,1},{3,2},{5,2},{6,2},{5,3},{6,3},{5,4},{6,4},{6,5},{1,6},{2,3},{2,5},{2,6},{3,5},{3,6},{4,5},{4,6},{5,6}}

Example: All permutations of four elements

The six possible inversions of a 4-element permutation

The following sortable table shows the 24 permutations of four elements with their place-based inversion sets, inversion related vectors and inversion numbers.

It is shown twice, so different orders can be compared to each other. (The Python script used to create it is shown here.)

The columns with small text are the reflections of the main columns. Sorting by them gives the colexicographic order of the corresponding main column.

Inversion vector Template:Invvect and left inversion count Template:Invvect are shown next to each other, because they have the same digits.

Left and right inversion counts are related to the place-based inversion sets shown between them:
The nontrivial elements of Template:Invvect are the sums of the descending diagonals of the triangle, and those of Template:Invvect are the sums of the of the ascending diagonals.

The default order of the table is the reverse colex order by $\pi$, which is the same as the colex order by Template:Invvect. (This header cell is highlighted by a darker gray.)

Lex order by $\pi$ is the same as lex order by Template:Invvect.

Ordering one table by Template:Invvect and the other one by Template:Invvect brings inverse permutations next to each other, i.e. those whose matrices are reflected at the main diagonal.

Ordering one table by reflected Template:Invvect and the other one by Template:Invvect brings permutations next to each other whose permutation matrices are reflected at the antidiagonal.

Ordering one table by reflected Template:Invvect and the other one by Template:Invvect brings permutations next to each other whose permutation matrices are rotated by 180°.
(It can be seen, that these permutations' inversion sets are symmetric to each other, which corresponds to Template:Invvect and Template:Invvect being symmetric to each other.)

Note that the set of all Template:Invvect, the set of all Template:Invvect and the set of all reflected Template:Invvect for the same symmetric group are equal.
So sorting by two columns that have the omissible 0 at the same end makes these columns equal.

3-element permutations
Template:3-el perm inversions Template:3-el perm inversions

Template:4-el perm inversions

Template:4-el perm inversions

(A more detailled version of this table, including element-based inversion sets and the unused fourth vector, can be found here.)

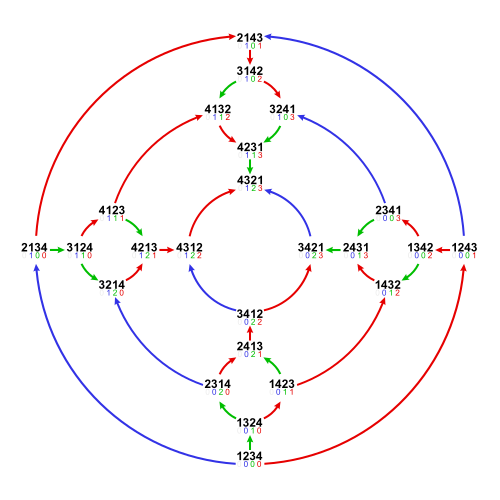
Weak order of permutations

The Hasse diagram below in the middle shows the 24 inversion sets ordered by the subset relation.

If a permutation is assigned to each inversion set using the place-based definition, the resulting order of permutations is that of the permutohedron,
where $(\pi ,\sigma )$ is an edge iff $i<j\wedge \pi (i)+1=\pi (j)\wedge (ij)\cdot \pi =\sigma$, i.e. when only two elements with consecutive values are swapped.
(In the central diagram it can be seen on which positions the swapped elements are, by looking which digit changes for the edge.)

The bitwise $\le$ ordering of the left and right inversion counts of these permutations gives the same order (because both are diagonal sums of the inversion set triangles).

Permutations and left inversion counts Template:Invvect

Inversion sets (place-based)

Permutations and right inversion counts Template:Invvect

Schlegel diagrams of the permutohedra above
Permutations and left inversion counts Template:Invvect Inversion sets (place-based) Permutations and right inversion counts Template:Invvect

If a permutation were assigned to each inversion set using the element-based definition, the resulting order of permutations would be that of a Cayley graph,
where $(\pi ,\sigma )$ is an edge iff $i+1=j\wedge \pi (i)<\pi (j)\wedge (ij)\cdot \pi =\sigma$, i.e. when only two elements on consecutive places are swapped.

This Cayley graph of the symmetric group is similar to its permutohedron, but with each permutation replaced by its inverse.

Cayley graph

Cayley graph as a Schlegel diagram The Cayley graph on the right shows the inverse permutations of those in the permutohedron above it. Below their Template:Invvect are shown. They are the same vectors as the Template:Invvect in the permutohedron above (because the Template:Invvect is the Template:Invvect of the inverse permutation). There are 12 edges of each color, and each represents the swapping of two elements on consecutive places — e.g. blue stands for the swapping of the elements on the first two places. The six squares of the truncated octahedron have blue and red edges, and the edges connecting the squares are green. Four of the eight hexagons have blue and four have red edges. Inverse permutations and inversion vectors Template:Invvect

Template:Rdrdo Inversions in sequences

For sequences inversion sets and the related vectors are not unique. Their place-based inversion sets are multisets, and their inversion vectors can have bigger digits than would be allowed in a factorial number.

Template:Rdrdo Arrays of permutations Template:Anchor

Error creating thumbnail:

Similar permutations have similar inversion sets and corresponding vectors.

Some can be ordered in arrays, like the one on the right, corresponding to the number triangle Template:Oeis.

Sources

Books

Cramer 1750

Cramer defines the inversion under the name dérangement to calculate the sign of a permutation.

For the permutation 3 1 2 the dérangements are given as 3 before 1 and 3 before 2.

Cramer, Gabriel: Introduction à l'analyse des lignes courbes algébriques. Genève : chez les Frères Cramer & Cl. Philibert 1750 — Appendice (p. 658)

Template:Cite book — 9.1 Cramers rule (p. 286)

Rothe 1800

Rothe essentially defines the right inversion count Template:Invvect under the name Stellenexponenten — but with each place bigger by 1.

$s_i$ is the position of ${\pi }_i$ among the ${\pi }_k$ with $k\ge i$ in numerical order. (p. 163)

Strangely he counts from 1 rather than 0, which later leads to avoidable additions and subtractions by 1:

$s_i+1=\mathrm{\#}\{{\pi }_k\mid k>i\wedge {\pi }_k<{\pi }_i\}$ (p. 165)

Each permutation has sign $+$ when the sum of the $s_i-1$ is even, and sign $-$ when it is odd. (p. 266)

For the permutation $64398101725$ the Stellenexponenten are given as $6436551311$.

Muir translates Stellenexponent as place-index and calls it “an ill-advised and purposeless modification of Cramers idea of a ‘derangement’”. (The Theory of the Determinant..., p. 55)

"Ueber Permutationen, in Beziehung auf die Stellen ihrer Elemente. Anwendung der daraus abgeleiteten Satze auf das Eliminationsproblem". In Hindenburg, Carl, ed., Sammlung Combinatorisch-Analytischer Abhandlungen, pp. 263–305, Bey G. Fleischer dem jüngern, 1800.

Laisant 1888

After defining the factorial number system Laisant defines the right inversion count Template:Invvect under the name signe figuratif.

For the permutation $436512$ the signe figuratif is given as $(32320)$.

Template:Citation

Aigner 2007

Now we look at permutations of $\{1,2,...,n\}$ in word form $\sigma =a_1,a_2...a_n,a_i=\sigma (i)$.
The pair $\{i,j\}$ is called an inversion if $i<j$ but $a_i>a_j$.

A moment's thought shows that $\{i,j\}$ is an inversion if and only if the edges $i{a}_i$ and $j{a}_j$ cross in the diagram.
Hence the inversion number $inv(\sigma )$ equals the number of crossings.

Template:Cite book — Word Representation (p. 27 ff)

Comtet 1974

An inversion of a permutation $\sigma \in 𝔖[n]$ is a pair $(i,j)$ such that $1\le i<j\le n$ and $\sigma (i)>\sigma (j)$. In this case we say that $\sigma$ has an inversion in $(i,j)$.

He uses the same definition for a non-bijective map in exercise 21 on permutations (p. 266).

Template:Cite book — 6.4 Inversions of a permutation of [n] (p. 237)

Cormen et al. 2001

Let $A[1..n]$ be an array of n distinct numbers. If $i<j$ and $A[i]>A[j]$, then the pair $(i,j)$ is called an inversion of $A$.

Template:Cite book — 2-4 Inversions (p. 41) and 5.2-5 (p. 122)

Knuth 1973

If $i<j$ and $a_i>a_j$, the pair $(a_i,a_j)$ is called an inversion of the permutation; for example the permutation 3 1 4 2 has three inversions: (3, 1), (3, 2) and (4, 2).

The inversion table $b_1{b}_2...b_n$ of the permutation $a_1{a}_2...a_n$ is obtained by letting $b_j$ be the number of elements to the left of $j$ that are greater than $j$.
In other words, $b_j$ is the number of inversions whose second component is $j$.

Template:Cite book — 5.1.1 Inversions (p. 11)

Pemmaraju & Skiena 2003

A pair of elements $(\pi (i),\pi (j))$ in a permutation $\pi$ represents an inversion if $i>j$ and $\pi (i)<\pi (j)$.
An inversion is a pair of elements that are out of order Template:Ellipsis

For any $n$-permutation $\pi$, we can define an inversion vector $v$ as follows. For each integer $i$, $1\le i\le n-1$, the $i$th element of $v$ is the number of elements in $\pi$ greater than $i$ to the left of $i$.

Template:Cite book — 2.2 Inversions and Inversion Vectors (p. 69)

Vitter & Flajolet 1990

An inversion in permutation $\sigma$ is an “out of order” pair $({\sigma }_k,{\sigma }_j)$ of elements, in which $k<j$ but ${\sigma }_k>{\sigma }_j$.
The number of inversions is thus a measure of the amount of disorder in a permutation.

The inversion table of the permutation $\sigma ={\sigma }_1{\sigma }_2\dots {\sigma }_n$ is the ordered sequence

$b_1,b_2,\dots ,b_n$, where $b_k=|\{1\le j<{\sigma }_k^{-}1|{\sigma }_j>k\}|$.

Template:Cite book — 3.1 Inversions (p. 459)

Grätzer 2016

Template:Textbox The authors define the usual strict linear ordering $1<2<\cdots <i<i+1<\cdots <n$ on $[n]$ as ${ℐ}_n=\{(i,j)\in [n]\times [n]|i<j\}$.

Let $\sigma$ be a permutation on $[n]$. An inversion of $\sigma$ is an ordered pair $(i,j)\in {ℐ}_n$ satisfying ${\sigma }^{-1}(i)>{\sigma }^{-1}(j)$.
The inversion set of $\sigma$ is then defined as $\mathrm{i}\mathrm{n}\mathrm{v}(\sigma )=\{(i,j)\in {ℐ}_n|{\sigma }^{-1}(i)>{\sigma }^{-1}(j)\}$.

The inversion set of $\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 3& 5& 4& 1& 2\end{array}\right)$ is given as $\{(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(4,5)\}$.

In the footnote it is mentioned that other authors often use the definition as an ordered pair $(i,j)\in {ℐ}_n$ such that $\sigma (i)>\sigma (j)$.
TAoCP is given as an example — despite the fact that Knuth uses essentially the same definition (see above).

Template:Cite book — 7-2 Basic objects (p. 221)

Joshi 1989

Let $x=x_1{x}_2\dots x_n$ be a sequence of real numbers.
By an inversion in $x$, we mean a pair $(x_i,x_j)$ such that $i<j$ but $x_i>x_j$.
For each $i$, let $d_i$ = the number of inversions whose first entry is $x_i$, i.e.

$d_i=|\{x_j:i<j,x_i>x_j\}|$.

Then the sequence $(d_1{d}_2\dots d_n)$ is called the inversion table or inversion vector of $x$. Template:Ellipsis
The permutation $24351$ has $(1,2,1,1,0)$ as its inversion table.

Template:Cite book — Definition 3.12 (p. 188)

Bóna 2012

Template:Textbox Bóna first uses the definition with elements:

Let $p=p_1{p}_2\cdots p_n$ be a permutation. We say that $(p_i,p_j)$ is an inversion of $p$ if $i<j$ but $p_i>p_j$.
Permutation 31524 has four inversions, namely (3, 1), (3, 2), (5, 2), and (5,4).

2.1 Inversions (p. 43)

Template:Textbox But for multisets he uses places instead:

An inversion of a permutation $p=p_1{p}_2\cdots p_n$ of a multiset is defined just as it was for permutations of sets, that is, $(i,j)$ is a inversion if $i<j$, but $p_i>p_j$·
The multiset-permutation 1322 has two inversions, (2, 3), and (2, 4).

2.2 Inversions in Permutations of Multisets (p. 57)

The definition of non-inversions also uses places:

Template:Ellipsis look at all non-inversions of a generic permutation $p=p_1{p}_2\cdots p_n$; that is, pairs so that $i<j$ and $p_i<p_j$.

4.4.1.1 An exponential upper bound (p. 141)

Template:Cite book

Calude et al. 2003

For permutations, an inversion vector is used as an auxiliary array because it fills in the holes made by the elements of the prefix in its defining sequence.
For the permutation $(p[i],\dots ,p[n])$ the right-inversion vector $(g[i],\dots ,g[n-1])$ is defined by the rule that $g[i]$ is the number of $p[j]$ to the right of but smaller than $p[i]$;
in the left-inversion vector, $g[i]$ is the number of $p[j]$ to the left of but larger than $p[i]$.

Template:Cite book — Generating Gray codes... (p. 81)

Lothaire 2002

If $\sigma =\sigma (1)\sigma (2)\dots \sigma (k)$ is [a permutation of $[k]$] an inversion of $\sigma$ is a pair $(i,j)$ such that $1\le i<j\le k$ and $\sigma (i)>\sigma (j)$.

11.1. Prelimiaries (p. 367)

Let $\sigma$ be a permutation of $[n]$. For $1\le i\le n$, let $l_i$ be the number of indices $j<i$ such that $\sigma (j)>\sigma (i)$. The word $l=l_1{l}_2\cdots l_n$ will be called the Lehmer encoding of $\sigma$.

To the permutation $\sigma =684593127$ corresponds the Lehmer encoding $l=002205662$.

11.4. Inversions of permutations with a given shape (p. 372)

Template:Cite book

Papers

Vajnovszki 2011

The pair $(i,j)$ is an inversion of $\pi \in {𝔖}_n$ if $i<j$ but ${\pi }_i>{\pi }_j$. Template:Ellipsis

An integer sequence $t_1{t}_2\dots t_n$ is said to be subexcedent if $0\le t_i\le i-1$ for $1\le i\le n$, and the set of lenth-$n$ subexcedent sequences is denoted by $S_n$ Template:Ellipsis.
The Lehmer code [5] is a bijection code : ${𝔖}_n\to S_n$ which maps each permutation $\pi ={\pi }_1{\pi }_2\dots {\pi }_n$ to a subexcedent sequence $t_1{t}_2\dots t_n$
where, for all $i,1\le i\le n$, $t_i$ is the number of inversions $(j,i)$ in $\pi$ (or equivalently, the number of entries in $\pi$ larger than ${\pi }_i$ and on its left).
[5]      D. H. Lehmer, Teaching combinatorial tricks to a computer, in Proc. Sympos. Appl. Math., 10 (1960), Amer. Math. Soc., 179-193.

Vajnovszki. A new Euler–Mahonian constructive bijection — pp. 1-2

Gnedin & Olshanski 2012

For $\sigma \in 𝔖$, a pair of positions $(i,j)\in \mathbb{Z}\times \mathbb{Z}$ is an inversion in $\sigma$ if $i<j$ and $\sigma (i)>\sigma (j)$.
If $(i,j)$ is an inversion, we say that it is a left inversion for $j$, and a right inversion for $i$.
Introduce the counts of left and right inversions,

${𝓁}_i:=\mathrm{\#}\{j:j<i,\sigma (j)>\sigma (i)\},{𝓇}_i:=\mathrm{\#}\{j:j>i,\sigma (j)<\sigma (i)\},i\in \mathbb{Z}$,

respectively (of course, for the general $\sigma \in 𝔖$ these quantities may be infinite).

4. A construction from independent geometric variables (p. 624)

The authors proof the following formula for balanced permutations, which include finite permutations:

$\sigma (i)=i+{𝓇}_i-{𝓁}_i,i\in \mathbb{Z}$

Lemma 4.6 (p. 627)

Gnedin; Olshanski. The two-sided infinite extension of the Mallows model for random permutations

Deutsch et al. 2008

In a permutation $\pi ={\pi }_1{\pi }_2\dots {\pi }_n$, an inversion is a pair $i<j$ such that ${\pi }_i>{\pi }_j$. Template:Ellipsis
If $c_i$ is the number of $j>i$ with ${\pi }_j<{\pi }_i$, then $(c_1,c_2,\dots ,c_n)$ is called the right inversion vector of $\pi$ Template:Ellipsis.

Deutsch; Pergola; Pinzani. Six bijections between deco polyominoes and permutations — p. 5

Barth & Mutzel 2004

File:Bilayer cross counting, non-map.svg

Crossings in a bilayer graph...

...correspond to inversions of a non-bijective map.

In a sequence $\pi =⟨a_0,a_1,\dots ,a_{t-1}⟩$ of pairwise comparable elements $a_i(i=0,1,\dots ,t-1)$, a pair $(a_i,a_j)$ is called an inversion if $i<j$ and $a_i>a_j$.

A crucial point of the article is illustrated by the images on the right: A bilayer graph that does not describe a map corresponds to a map that has the edges (green) as its domain and one layer of the vertices (blue) as its codomain. The number of crossings in the bilayer graph can be calculated as the number of inversions of the map.
In this example the map is $\pi =⟨0,1,2,0,3,4,0,2,3,2,4⟩$.

${\pi }_2=2$, ${\pi }_3=0$ and ${\pi }_6=0$, so with the place-based definition the sequence would have the inversions $(2,3)$ and $(2,6)$.
With the element-based definition, chosen by the authors, one could say that the sequence has the inversion $(2,0)$ twice.

Template:Cite journal — 2 Bilayer Cross Counts and Inversion Numbers (p. 183)