Noble Boolean functions

Template:Boolf header Template:Zhegalkin stuff Noble Boolean functions are those who are their own Zhegalkin twins, i.e. the binary expression of their ANF is equal to their truth table.
They correspond to Template:W in the Zhegalkin permutation.
They are all even, i.e. the first digit of their truth table is false.
When a Boolean function is noble, its whole faction is noble.
Within the this project it is slightly misleading to apply the term noble to Boolean functions. It is a property of a truth table with a specific length.

Template:Collapsible START Template:Collapsible END

Template:Collapsible START These matrices show the 2-ary and 3-ary Boolean functions, represented by the big gray integers (corresponding to the truth tables).
The small black integers above them are the senior nobles (i.e. one arity above).
(The highlighted big numbers are the king indices.)

Error creating thumbnail: 3-ary nobles

4-ary nobles

Template:Collapsible START File:Zhegalkin 256; fixed.svg Template:Collapsible END

row 3

row 4

Template:Clear The images show how ${\mathrm{\Phi }}_n$ is derived from ${\mathrm{\Pi }}_{n-1}$, the permutation of the same length.
The long matrices have two halves:
In the upper half the bit pattern in column $k$ is that of ${\mathrm{\Xi }}_{n-1,k}={\mathrm{\Pi }}_{n-1,k}\oplus k$.    (Compare triangle Ξ in the next section.)
The bit pattern in the lower half is identical to that of the gray column indices.

${\mathrm{\Phi }}_{n,k}={\mathrm{\Xi }}_{n-1,k}+(2^{2^{n-1}}\cdot k)=({\mathrm{\Pi }}_{n-1,k}\oplus k)+(2^{2^{n-1}}\cdot k)$

The small matrices on the left are divided in the same way:
The upper half is a Sierpiński triangle without the main diagonal, and the lower half is the main diagonal.

These properties of noble Boolean functions can be derived from this:

• They are even, i.e. place 0 is always false.
• The 1-bit places (e.g. 1, 2, 4, 8) have the same truth value. (Those where it is false/true shall be called weak/strong.)
• Half of them are evil/odious, which is indicated by the last place being false/true. (The odious ones are on the right, just like in triangle Π.)

Template:Collapsible START The row sum of ${\mathrm{\Phi }}_n$ for $n\ge 1$ is $2^a\cdot (2^b-1)=2^{a+b}-2^a$ with $a=2^{n-1}$ and $b=2^n-1$.
That is a binary number consisting of $a$ 0s at the little and $b$ 1s at the big end.

E.g. that of ${\mathrm{\Phi }}_2$ is 0 + 6 + 8 + 14 = 28. (11100 as a binary number.)

n	sum of row n
0		1
1	$2^1\cdot (2^1-1)=2^2-2^1$	2
2	$2^2\cdot (2^3-1)=2^5-2^2$	28
3	$2^4\cdot (2^7-1)=2^{11}-2^4$	2032
4	$2^8\cdot (2^{15}-1)=2^{23}-2^8$	8388352
5	$2^{16}\cdot (2^{31}-1)=2^{47}-2^{16}$	140737488289792

quadrants

It is easily seen, that the left and right half of each row differ only in the last digit.
Those on the left/right have even/odd weight. They shall be called evil/odious.

There are two ways to derive one half from the other.

Let $L$ be the left (evil) and $R$ be the right (odious) half.
Let $p=2^{(2^n-1)}$ be the unique power of two, and $q=2^{2^n}-2$ be the highest entry.   (They are the first and last entries of $R$.)
Let $j$ be the mirrored index of $i$.   ($j$ is as far from the right as $i$ is from the left.)

Then $R_i=L_i+p=q-L_j$. Template:Spaces (Template:W can be used instead of plus and minus.)

The following Python code illustrates this for rows 1 to 3:

left_and_right_half = {
    1: [
        [0], 
        [2]
    ],
    2: [
        [0,  6], 
        [8, 14]
    ],
    3: [
        [  0,  30,  40,  54,  72,  86,  96, 126], 
        [128, 158, 168, 182, 200, 214, 224, 254]
    ]
}

for n, (left, right) in left_and_right_half.items():
    length = 2 ** (2 ** (n - 1) - 1)
    p = 2 ** (2 ** n - 1)
    q = 2 ** (2 ** n) - 2
    for i in range(length):
        j = length - i - 1
        assert right[i] == left[i] + p == q - left[j]
        assert right[i] == left[i] ^ p == q ^ left[j]

There is a second way to partition the nobles in two halves:
Those in even/odd places of the triangle row have false/true entries in all 1-bit places of their truth table. They shall be called weak/strong.

So the nobles can be partitioned into four quadrants by depravity and strength.

Template:Collapsible START Vertically adjacent quadrants contain relative complements. Horizontally adjacent quadrants differ only in the central vertex.
(40 and 214 are relative complements. 40 and 168 differ only in the central vertex.)

The 16 noble 3-ary Boolean functions form 8 factions. So there are 2 royal factions.

Error creating thumbnail:

Nobles that are evil and weak shall be called royal.
Each noble corresponds to a royal, and can easily be derived from it. (A royal corresponds to itself.)
When a Boolean function is royal, its whole faction is royal.
The function with the smallest Zhegalkin index in a faction shall be called king, and be used to represent it.
So all nobles of a given arity can effectively be represented by a rather short list of kings.

Template:Collapsible START The columns of this matrix are the 4-ary royal Boolean functions.
Error creating thumbnail:
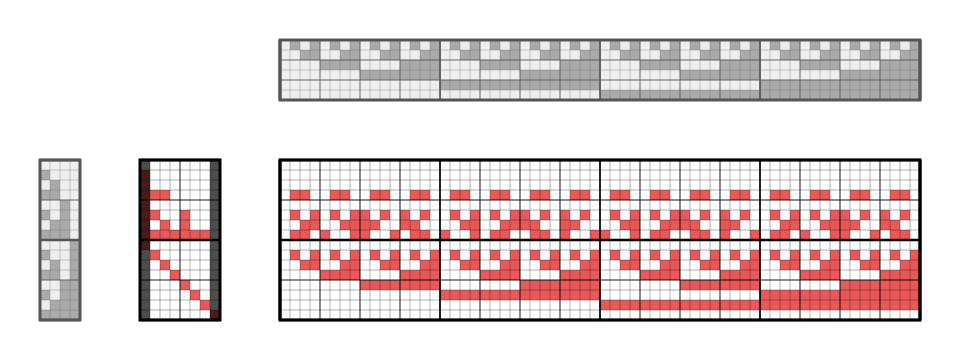
Compare ${\mathrm{\Phi }}_4$ as 16×256 matrix, shown above.
The 16×6 matrix on the left is shown as the 16×8 matrix from that file, with the left and right column blacked out. Template:Collapsible END

triangle of kings

Number of royal factions for arities 0...5: Template:Spaces 1, 1, 1, 2, 11, 272 This triangle shows the representatives of each royal faction. 0 1 2 3 4 [0] [0] [0] [0, 40] [0, 680, 1632, 2176, 3808, 5760, 6856, 10920, 11464, 26752, 28384] row 5 of length 272:     0, 174760, 419424 ... 2091314912, 2091559592, 2093664936 [0, 174760, 419424, 559232, 664104, 978656, 1480320, 1603680, 1757896, 2631680, 2785960, 2942152, 3034720, 4112000, 6875264, 7245536, 8289792, 8421376, 8840800, 9085480, 10025056, 10395136, 11053056, 11456096, 16711168, 18245760, 18384480, 18492616, 18800640, 19453440, 19561640, 19837024, 20769320, 23772200, 25067520, 25351336, 25753216, 26667136, 26913992, 27983016, 36208640, 36317864, 36457672, 36628064, 37534760, 37775488, 37929512, 38330368, 38700640, 39081128, 39255552, 39500360, 39640104, 39745152, 40561192, 40668232, 41712808, 41866752, 42107560, 42263752, 42508416, 42911456, 43433600, 43711176, 43818152, 44739240, 44879048, 46196864, 46844584, 47502504, 48166528, 50134184, 54454400, 56159968, 56526976, 57196160, 57596128, 58491560, 58775040, 59158624, 59438120, 60090920, 60337760, 60737536, 61406720, 62702120, 63232584, 63895648, 107129512, 107513984, 107933408, 108435072, 108558432, 108712648, 109109248, 109479520, 109756968, 110279240, 110663776, 111083008, 111340072, 111724544, 112111200, 112242784, 112645632, 113046568, 115795552, 116979808, 125339232, 125755392, 126006440, 126391936, 126808288, 126938848, 127585480, 127975040, 128375008, 128776904, 129164488, 132707968, 142781096, 143165568, 143584992, 143716576, 144086656, 144364232, 144744576, 145147616, 145548488, 145947336, 146331872, 146718336, 149481600, 150402688, 160605256, 161406976, 161674280, 162059776, 162443360, 163375656, 166131808, 178430504, 178570312, 179234400, 179370080, 180017736, 180141096, 180936704, 181861888, 182246440, 183167528, 183825448, 197060736, 198766304, 199555784, 250539744, 250671328, 375941248, 376095272, 377421312, 377662120, 378046592, 378466016, 378967680, 379245256, 380429512, 381599360, 384362624, 394329600, 394696800, 394976296, 396288000, 398256680, 411099136, 411469408, 411746856, 412269128, 412653664, 413072896, 413329960, 413714432, 414101088, 414232672, 414635520, 415036456, 417785440, 418969696, 428928736, 429575368, 429964928, 430364896, 430766792, 431154376, 434697856, 446752896, 447400616, 447524040, 447918792, 448058536, 448722560, 449244896, 450024136, 450425056, 451208392, 452655816, 464578144, 467066880, 468382760, 518053888, 520027648, 679510016, 679929440, 680174120, 680313928, 680836136, 681113696, 682141696, 682544736, 683862568, 684247040, 685168128, 685569064, 687799808, 697755776, 698002632, 698141352, 699071656, 700366976, 700897504, 701299400, 715827880, 715967688, 717285504, 717933224, 718591144, 719255168, 721222824, 733790760, 734321224, 734984288, 751234784, 751619272, 752014024, 752414944, 753198280, 754645704, 769056768, 770372648, 786884192, 788068448, 1019396648, 1019797504, 1020722688, 1022028328, 1037627104, 1055451264, 1753393832, 1753778304, 1754197728, 1754699392, 1754976968, 1756161224, 1757331072, 1760094336, 1772019712, 1773988392, 1789847136, 1791549440, 1793780264, 1807673472, 1809379040, 1861152480] Finding the next row would require looping through the $2^{30}$ (slightly more than a billion) 6-ary royal Boolean functions.

Template:Collapsible START Error creating thumbnail:

The top left corner in each 2×2 matrix is a king. The other corners are its equivalents in the other quadrants.
(Vertically adjacent quadrants contain relative complements. Horizontally adjacent quadrants differ only in the central vertex.)

The two tables below correspond to the image above. The one on the left shows the same numbers as the image.
The one on the right shows the smallest Zhegalkin index for each of the 44 factions. (They differ only for the odd factions, i.e. those with green and blue background.)

Template:Noble reps/outer/match

Template:Noble reps/outer/minimal

The black integers are Zhegalkin indices. The gray numbers below are their noble indices, i.e. the positions in the sequence of nobles.
The beige numbers in the image are faction sizes, i.e. the number of different permutations of the example shown. Template:Collapsible END

Template:Collapsible START Error creating thumbnail: Template:Collapsible END

group under exclusive or

With XOR as a group operation the n-ary noble and royal Boolean functions form a power of the Template:W C₂.

Template:Collapsible START The 3-ary nobles form the group C₂⁴.

The Python operator ^ represents the Template:W.

nobles = [0,  30,  40, 54,  72, 86, 96, 126, 128, 158, 168, 182, 200, 214, 224, 254]

for i, a in enumerate(nobles):
    for j, b in enumerate(nobles):
        assert nobles.index(a ^ b) == i ^ j

This works for any row of the noble triangle $\mathrm{\Phi }$, or from the royal triangle. (But not from the triangle of kings.) Template:Collapsible END

patrons

The XOR of twins is noble, i.e. the XOR of a key and a value in ${\mathrm{\Pi }}_n$ is an entry of ${\mathrm{\Phi }}_n$.
For a Boolean function this means, that the XOR of its ANF and its truth table is a noble Boolean function, which shall be called its patron.
The patron of a noble is the contradiction.

${\mathrm{\Xi }}_{n,k}={\mathrm{\Pi }}_{n,k}\oplus k$

k 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 n 0 0 0 1 0 2 0 2 2 0 14 8 6 8 6 0 14 0 14 8 6 8 6 0 14 row 3 of length 256:     0, 254, 168, 86 ... 168, 86, 0, 254 [0, 254, 168, 86, 200, 54, 96, 158, 128, 126, 40, 214, 72, 182, 224, 30, 224, 30, 72, 182, 40, 214, 128, 126, 96, 158, 200, 54, 168, 86, 0, 254, 128, 126, 40, 214, 72, 182, 224, 30, 0, 254, 168, 86, 200, 54, 96, 158, 96, 158, 200, 54, 168, 86, 0, 254, 224, 30, 72, 182, 40, 214, 128, 126, 128, 126, 40, 214, 72, 182, 224, 30, 0, 254, 168, 86, 200, 54, 96, 158, 96, 158, 200, 54, 168, 86, 0, 254, 224, 30, 72, 182, 40, 214, 128, 126, 0, 254, 168, 86, 200, 54, 96, 158, 128, 126, 40, 214, 72, 182, 224, 30, 224, 30, 72, 182, 40, 214, 128, 126, 96, 158, 200, 54, 168, 86, 0, 254, 0, 254, 168, 86, 200, 54, 96, 158, 128, 126, 40, 214, 72, 182, 224, 30, 224, 30, 72, 182, 40, 214, 128, 126, 96, 158, 200, 54, 168, 86, 0, 254, 128, 126, 40, 214, 72, 182, 224, 30, 0, 254, 168, 86, 200, 54, 96, 158, 96, 158, 200, 54, 168, 86, 0, 254, 224, 30, 72, 182, 40, 214, 128, 126, 128, 126, 40, 214, 72, 182, 224, 30, 0, 254, 168, 86, 200, 54, 96, 158, 96, 158, 200, 54, 168, 86, 0, 254, 224, 30, 72, 182, 40, 214, 128, 126, 0, 254, 168, 86, 200, 54, 96, 158, 128, 126, 40, 214, 72, 182, 224, 30, 224, 30, 72, 182, 40, 214, 128, 126, 96, 158, 200, 54, 168, 86, 0, 254]

For $n\ge 1$ the entries in ${\mathrm{\Xi }}_n$ are repetitions of those in ${\mathrm{\Phi }}_n$. E.g. ${\mathrm{\Xi }}_2$ contains the entries $\{0,6,8,14\}$, each repeated four times.

The set of places where ${\mathrm{\Xi }}_n$ has entries ${\mathrm{\Phi }}_{n,k}$ can be calculated by XORing ${\mathrm{\Pi }}_{n-1,k}$ with the entries of ${\mathrm{\Phi }}_n$.

3-ary Boolean functions with patron 168

Template:Collapsible START Let $\pi ={\mathrm{\Pi }}_2$ (length 16), $\varphi ={\mathrm{\Phi }}_3$ (length 16) and $\xi ={\mathrm{\Xi }}_3$ (length 256).
Let $I_k=\{i\mid {\xi }_i={\varphi }_k\}$ be the set of places where $\xi$ has the entry ${\varphi }_k$.

$\pi$ is the left column of the following matrix.
$\varphi$ is its top row, and also shown in the column to its right.
The matrix entries are the bitwise XORs of its left column and top row.
$I_k$ is row $k$ as a set of numbers: $\{{\pi }_k\oplus f\mid f\in \varphi \}$

Example:   In which places is $\xi$ equal to ${\varphi }_{10}=168$?
${\pi }_{10}=2⟹I_{10}=\{2\oplus f\mid f\in \varphi \}=\{2,28,...,226,252\}$
It can be easily seen, that the first and the last entry 168 in $\xi$ is in places 2 and 252.

0	0	30	40	54	72	86	96	126	128	158	168	182	200	214	224	254		0
1	15	17	39	57	71	89	111	113	143	145	167	185	199	217	239	241		30
2	10	20	34	60	66	92	106	116	138	148	162	188	194	220	234	244		40
3	5	27	45	51	77	83	101	123	133	155	173	179	205	211	229	251		54
4	12	18	36	58	68	90	108	114	140	146	164	186	196	218	236	242		72
5	3	29	43	53	75	85	99	125	131	157	171	181	203	213	227	253		86
6	6	24	46	48	78	80	102	120	134	152	174	176	206	208	230	248		96
7	9	23	33	63	65	95	105	119	137	151	161	191	193	223	233	247		126
8	8	22	32	62	64	94	104	118	136	150	160	190	192	222	232	246		128
9	7	25	47	49	79	81	103	121	135	153	175	177	207	209	231	249		158
10	2	28	42	52	74	84	98	124	130	156	170	180	202	212	226	252		168
11	13	19	37	59	69	91	109	115	141	147	165	187	197	219	237	243		182
12	4	26	44	50	76	82	100	122	132	154	172	178	204	210	228	250		200
13	11	21	35	61	67	93	107	117	139	149	163	189	195	221	235	245		214
14	14	16	38	56	70	88	110	112	142	144	166	184	198	216	238	240		224
15	1	31	41	55	73	87	97	127	129	159	169	183	201	215	225	255		254

The lower 8×16 matrix corresponds to row 10.
The one above contains the Zhegalkin indices, and has the same set of columns.

Nobles for comparison

File:3-ary Boolean functions; patrons 10.svg

Boolean functions with patron 168 in octeract matrix
(This is the transpose of Zhegalkin indices with quaestor 3.)