OpenStax University Physics/V1/Equations (master)

Equations (master) | Formulas (master) | Equations | Formulas | College Physics

Equations inspired by the Chapter Summaries of OpenStax University Physics Volume 1. Instructors who wish to base their course notes on Wikiversity should not use this version, but instead copy this much more user-friendly that contains easily understood transclusions to this "master". A four-page summary suitable for use during in-class exams is available in two different versions: "master" (online viewing) and "compact". The "compact" version is also available in this pdf form.

<section begin=Introduction/>

Introduction

metric prefixes

da	h	k	M	G	T	P	E	Z	Y
deca	hecto	kilo	mega	giga	tera	peta	exa	zetta	yotta
1E+01	1E+02	1E+03	1E+06	1E+09	1E+12	1E+15	1E+18	1E+21	1E+24
d	c	m	µ	n	p	f	a	z	y
deci	centi	milli	micro	nano	pico	femto	atto	zepto	yocto
1E-01	1E-02	1E-03	1E-06	1E-09	1E-12	1E-15	1E-18	1E-21	1E-24

<section end=Introduction/> <section begin=Units_and_Measurement/>

Units_and_Measurement

The base SI units are mass: kg (kilogram); length: m (meter); time: s (second). Percent error is $(\delta A/A)\times 100\mathrm{\%}$

<section end=Units_and_Measurement/> <section begin=Vectors/>

Vectors

Vector $\overrightarrow{A}=A_x\hat{i}+A_y\hat{j}+A_z\hat{k}$ involves components (A_x,A_y,A_z) and three orthonormal unit vectors.

▭ If $\overrightarrow{A}+\overrightarrow{B}=\overrightarrow{C}$, then A_x+B_x=C_x, etc, and vector subtraction is defined by $\overrightarrow{B}=\overrightarrow{C}-\overrightarrow{A}$.

▭ The two-dimensional displacement from the origin is $\overrightarrow{r}=x\hat{i}+y\hat{j}$. The magnitude is $A\equiv |\overrightarrow{A}|=\sqrt{A_x^2+A_y^2}$. The angle (phase) is $\theta ={\tan }^{-1}(y/x)$.

▭ Scalar multiplication $\alpha \overrightarrow{A}=\alpha A_x\hat{i}+\alpha A_y\hat{j}+...$

▭ Any vector divided by its magnitude is a unit vector and has unit magnitude: $|\hat{V}|=1$ where $\hat{V}\equiv \overrightarrow{V}/V$

▭ Dot product $\overrightarrow{A}\cdot \overrightarrow{B}=AB\cos \theta =A_x{B}_x+A_y{B}_y+...$ and $\overrightarrow{A}\cdot \overrightarrow{A}=A^2$

▭ Cross product $\overrightarrow{A}=\overrightarrow{B}\times \overrightarrow{C}\Rightarrow$ $A_{\alpha }=B_{\beta }{C}_{\gamma }-C_{\gamma }{A}_{\beta }$ where $(\alpha ,\beta ,\gamma )$ is any cyclic permutation of $(x,y,z)$, i.e., (α,β,γ) represents either (x,y,z) or (y,z,x) or (z,x,y).

▭ Template:Nowrap magnitudes obey $A=BC\sin \theta$ where $\theta$ is the angle between $\overrightarrow{B}$ and $\overrightarrow{C}$, and $\overrightarrow{A}\perp \{\overrightarrow{B},\overrightarrow{C}\}$ by the right hand rule.

▭ Vector identities $c(𝐀+𝐁)=c𝐀+c𝐁$

▭ $𝐀+𝐁=𝐁+𝐀$

▭ $𝐀+(𝐁+𝐂)=(𝐀+𝐁)+𝐂$

▭ $𝐀\cdot 𝐁=𝐁\cdot 𝐀$

▭ $𝐀\times 𝐁=\mathbf{-}𝐁\times 𝐀$

▭ $(𝐀+𝐁)\cdot 𝐂=𝐀\cdot 𝐂+𝐁\cdot 𝐂$

▭ $(𝐀+𝐁)\times 𝐂=𝐀\times 𝐂+𝐁\times 𝐂$

▭ $𝐀\cdot (𝐁\times 𝐂)=𝐁\cdot (𝐂\times 𝐀)=(𝐀\times 𝐁)\cdot 𝐂$

▭ $𝐀\mathbf{\times }(𝐁\times 𝐂)=(𝐀\cdot 𝐂)𝐁-(𝐀\cdot 𝐁)𝐂$

▭ $(A\times B)\mathbf{\cdot }(𝐂\times 𝐃)=(𝐀\cdot 𝐂)(𝐁\cdot 𝐃)-(𝐁\cdot 𝐂)(𝐀\cdot 𝐃)$ <section end=Vectors/> <section begin=Motion_Along_a_Straight_Line/>

Motion_Along_a_Straight_Line

Delta as difference $\mathrm{\Delta }x=x_f-x_i\to dx\to 0$ in limit of differential calculus.

▭ Average velocity $\overline{v}=\mathrm{\Delta }x/\mathrm{\Delta }t\to v=dx/dt$ (instantaneous velocity)

▭ Acceleration $\overline{a}=\mathrm{\Delta }v/\mathrm{\Delta }t\to a=dv/dt$.

▭ WLOG set $\mathrm{\Delta }t=t$ and $\mathrm{\Delta }x=x-x_0$ if $t_i=0$. Then $\mathrm{\Delta }v=v-v_0$, and $v(t)=\underset{0}{\overset{t}{\int }}a(t^{\prime })d{t}^{\prime }+v_0$, $x(t)=\underset{0}{\overset{t}{\int }}v(t^{\prime })d{t}^{\prime }+x_0=x_0+\overline{v}t$, where $\overline{v}=\frac{1}{t}\underset{0}{\overset{t}{\int }}v(t^{\prime })d{t}^{\prime }$ is the average velocity.

▭ At constant acceleration: $\overline{v}=\frac{v_0+v}{2},v=v_0+at,x=x_0+v_{0}t+\frac{1}{2}a{t}^2,$ $v^2=v_0^2+2a\mathrm{\Delta }x$.

▭ For free fall, replace $x\to y$ (positive up) and $a\to -g$, where $g$ = 9.81 m/s² at Earth's surface). <section end=Motion_Along_a_Straight_Line/> <section begin=Motion_in_Two_and_Three_Dimensions/>

Motion_in_Two_and_Three_Dimensions

Instantaneous velocity: $\overrightarrow{v}(t)=v_x(t)\hat{i}+v_y(t)\hat{j}+v_z(t)\hat{k}=\frac{dx}{dt}\hat{i}+\frac{dy}{dt}\hat{j}+\frac{dz}{dt}\hat{k}$ $=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\mathrm{\Delta }\overrightarrow{r}}{\mathrm{\Delta }t}=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\overrightarrow{r}(t+\mathrm{\Delta }t)-\overrightarrow{r}(t)}{\mathrm{\Delta }t}$, where $\overrightarrow{r}(t)=x(t)\hat{i}+y(t)\hat{j}+z(t)\hat{k}$

▭ Acceleration $\overrightarrow{a}=a_x\hat{i}+a_y\hat{j}+a_z\hat{k}$, where $a_x(t)=d{v}_x/dt=d^{2}x/d{t}^2$.

▭ Average values: ${\overrightarrow{v}}_{ave}=\frac{\mathrm{\Delta }\overrightarrow{r}}{\mathrm{\Delta }t}=\frac{\overrightarrow{r}(t_2)-\overrightarrow{r}(t_2)}{t_2-t_1}$, and ${\overrightarrow{a}}_{ave}=\frac{\mathrm{\Delta }\overrightarrow{v}}{\mathrm{\Delta }t}=\frac{\overrightarrow{v}(t_2)-\overrightarrow{v}(t_2)}{t_2-t_1}$

▭ Free fall time of flight $T_{of}=\frac{2(v_0\sin {\theta }_0)}{g},$ ▭ Trajectory $y=(\tan {\theta }_0)x-\left[\frac{g}{2(v_0\cos {\theta }_0{)}^2}\right]x^2,$ ▭ Range $R=\frac{v_0^2\sin 2{\theta }_0}{g}$

▭ Uniform circular motion: $|\overrightarrow{a}|=a_C={\omega }^{2}r=v^2/r$ where $v\equiv |\overrightarrow{v}|=\omega r$

$\overrightarrow{r}=A\cos \omega t\hat{i}+A\sin \omega t\hat{j},$ $\overrightarrow{v}=-A\omega \sin \omega t\hat{i}+A\omega \cos \omega t\hat{j},$ $\overrightarrow{a}=-A{\omega }^2\cos \omega t\hat{i}-A{\omega }^2\sin \omega t\hat{j}.$

▭ Tangential and centripetal acceleration $\overrightarrow{a}={\overrightarrow{a}}_c+{\overrightarrow{a}}_T$ where $a_T=d|\overrightarrow{v}|/dt$.

▭ Relative motion: ${\overrightarrow{r}}_{PS}={\overrightarrow{r}}_{P{S}^{\prime }}+{\overrightarrow{r}}_{S^{\prime }S}$, ${\overrightarrow{v}}_{PS}={\overrightarrow{v}}_{P{S}^{\prime }}+{\overrightarrow{v}}_{S^{\prime }S}$, ${\overrightarrow{v}}_{PC}={\overrightarrow{v}}_{PA}+{\overrightarrow{v}}_{AB}+{\overrightarrow{v}}_{BC}$, ${\overrightarrow{a}}_{PS}={\overrightarrow{a}}_{P{S}^{\prime }}+{\overrightarrow{a}}_{S^{\prime }S}$ <section end=Motion_in_Two_and_Three_Dimensions/> <section begin=Newton's_Laws_of_Motion/>

Newton's_Laws_of_Motion

Newton's 2^nd Law $m\overrightarrow{a}=d\overrightarrow{p}/dt=\sum {\overrightarrow{F}}_j$, where $\overrightarrow{p}=m\overrightarrow{v}$ is momentum, $m$ is mass, and $\sum {\overrightarrow{F}}_j$ is the sum of all forces This sum needs only include external forces because all internal forces cancel by the 3^rd law ${\overrightarrow{F}}_{AB}=-{\overrightarrow{F}}_{BA}$. The 1^st law is that velocity is constant if the net force is zero.

▭ Weight$=\overrightarrow{w}=m\overrightarrow{g}$.

▭ normal force is a component of the contact force by the surface. If the only forces are contact and weight, $|\overrightarrow{N}|=N=mg\cos \theta$ where $\theta$ is the angle of incline.

▭ Hooke's law $F=-kx$ where $k$ is the spring constant. <section end=Newton's_Laws_of_Motion/>

<section begin=Applications_of_Newton's_Laws/>

Applications_of_Newton's_Laws

$f_s\le {\mu }_{s}N\text{ and }{f}_k={\mu }_{k}N$: $f=$ friction, ${\mu }_{s,k}=$ coefficient of (static,kinetic) friction, $N=$ normal force.

▭ Centripetal force$F_c=m{v}^2/r=mr{\omega }^2$ for uniform circular motion. Angular velocity $\omega$ is measured in radians per second.

▭ Ideal angle of banked curve: $\tan \theta =v^2/(rg)$ for curve of radius $r$ banked at angle $\theta$.

▭ Drag equation $F_D=\frac{1}{2}C\rho A{v}^2$ where $C=$ Drag coefficient, $\rho =$ mass density, $A=$ area, $v=$ speed. Holds approximately for large Reynold's number $=\mathrm{R}\mathrm{e}=\rho vL/\eta$, where $\eta =$dynamic viscosity; $L=$ characteristic length.

▭ Stokes's law models a sphere of radius $r$ at small Reynold's number: $F_s=6\pi r\eta v$. <section end=Applications_of_Newton's_Laws/> <section begin=Work_and_Kinetic_Energy/>

Work_and_Kinetic_Energy

Infinitesimal work done by force: $dW=\overrightarrow{F}\cdot d\overrightarrow{r}=|\overrightarrow{F}||d\overrightarrow{r}|\cos \theta$ leads to the path integral $W_{AB}=\underset{A}{\overset{B}{\int }}\overrightarrow{F}\cdot d\overrightarrow{r}$

▭ Work done from A→B by friction $-f_k|{\ell }_{AB}|,$gravity $-mg(y_B-y_A),$ and spring $-\frac{1}{2}k(x_B^2-x_A^2)$

▭ Work-energy theorem: The work done on a particle is $W_{net}=K_B-K_A$ where kinetic energy $=K=\frac{1}{2}m{v}^2=\frac{p^2}{2m}$.

▭ Power$=P=dW/dt=\overrightarrow{F}\cdot \overrightarrow{v}$. <section end=Work_and_Kinetic_Energy/> <section begin=Potential_Energy_and_Conservation_of_Energy/>

Potential_Energy_and_Conservation_of_Energy

Potential Energy: $\mathrm{\Delta }{U}_{AB}=U_B-U_A=-W_{AB}$; PE at $\overrightarrow{r}$ WRT ${\overrightarrow{r}}_0$ is $\mathrm{\Delta }U=U(\overrightarrow{r})-U({\overrightarrow{r}}_0)$

$U=mgy+𝒞$ (gravitational PE Earth's surface. $U=\frac{1}{2}k{x}^2+𝒞$ (ideal spring)

▭ Conservative force: $\oint {\overrightarrow{F}}_{\text{cons}}\cdot d\overrightarrow{r}=0$. In 2D, $\overrightarrow{F}(x,y)$ is conservative if and only if $\overrightarrow{F}=-(\partial U/\partial x)\hat{i}-(\partial U/\partial y)\hat{j}⟺\partial F_x/\partial y=\partial F_y/\partial x$

▭ Mechanical energy is conserved if no non-conservative forces are present: $0=W_{nc,AB}=\mathrm{\Delta }(K+U{)}_{AB}=\mathrm{\Delta }{E}_{AB}$ <section end=Potential_Energy_and_Conservation_of_Energy/>

<section begin=Linear_Momentum_and_Collisions/>

Linear_Momentum_and_Collisions

$\overrightarrow{F}(t)=d\overrightarrow{p}/dt\text{, where }\overrightarrow{p}=m\overrightarrow{v}$ is momentum.

▭ Impulse-momentum theorem $\overrightarrow{J}=F_{ave}\mathrm{\Delta }t=\underset{t_i}{\overset{t_f}{\int }}\overrightarrow{F}dt=\mathrm{\Delta }\overrightarrow{p}$.

▭ For 2 particles in 2D $\text{If }{\overrightarrow{F}}_{ext}=0\text{ then }\sum _{j=1}^N{\overrightarrow{p}}_j=0\Rightarrow p_{f,\alpha }=p_{1,i,\alpha }+p_{2,i,\alpha }$ where (α,β)=(x,y)

▭ Center of mass: ${\overrightarrow{r}}_{CM}=\frac{1}{M}\sum _{j=1}^N{m}_j{\overrightarrow{r}}_j\to \frac{1}{M}\int \overrightarrow{r}dm,$ ${\overrightarrow{v}}_{CM}=\frac{d}{dt}{\overrightarrow{r}}_{CM}$, and ${\overrightarrow{p}}_{CM}=\sum _{j=1}^N{m}_j{\overrightarrow{v}}_j=M{\overrightarrow{v}}_{CM}.$

▭ $\overrightarrow{F}=\frac{d}{dt}{\overrightarrow{p}}_{CM}=m{\overrightarrow{a}}_{CM}=\sum _{j=1}^N{m}_j{\overrightarrow{a}}_j$

▭ Rocket equation $mdv=-udm\Rightarrow \mathrm{\Delta }v=u\ln (m_f/m_i)$ where u is the gas speed WRT the rocket. <section end=Linear_Momentum_and_Collisions/> <section begin=Fixed-Axis_Rotation/>

Fixed-Axis_Rotation

$\theta =s/r$ is angle in radians,$\omega =d\theta /dt$ is angular velocity;

▭ $v_t=\omega r=ds/dt$ is tangential speed. Angular acceleration is $\alpha =d\omega /dt=d^2\theta /d{t}^2$. $a_t=\alpha r=d^{2}s/d{t}^2$ is the tangential acceleration.

▭ Constant angular acceleration $\overline{\omega }=\frac{1}{2}({\omega }_0+{\omega }_f)$ is average angular velocity.

▭ ${\theta }_f={\theta }_0+\overline{\omega }t={\theta }_0+{\omega }_{0}t+\frac{1}{2}\alpha t^2.$

▭ ${\omega }_f={\omega }_0+\alpha t.$ ${\omega }_f^2={\omega }_0^2+2\alpha \mathrm{\Delta }\theta .$

▭ Total acceleration is centripetal plus tangential: $\overrightarrow{a}={\overrightarrow{a}}_c+{\overrightarrow{a}}_t.$

▭ Rotational kinetic energy is $K=\frac{1}{2}I{\omega }^2,$ where $I=\sum _j{m}_j{r}_j^2\to \int r^{2}dm$ is the Moment of inertia.

▭ parallel axis theorem $I_{parallel-axis}=I_{centerofmass}+m{d}^2$

▭ Restricting ourselves to fixed axis rotation, $r$ is the distance from a fixed axis; the sum of torques, $\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F}$ requires only one component, summed as ${\tau }_{net}=\sum {\tau }_j=\sum r_{{\perp }_j}{F}_j=I\alpha$.

▭ Work done by a torque is $dW=(\sum {\tau }_j)d\theta$. The Work-energy theorem is $K_B-K_A=W_{AB}=\underset{{\theta }_A}{\overset{{\theta }_B}{\int }}\left(\sum _j{\tau }_j\right)d\theta$.

▭ Rotational power $=P=\tau \omega$.

I=∫r²dm for a hoop, disk, cylinder, box, plate, rod, and spherical shell or solid can be found from this figure.

<section end=Fixed-Axis_Rotation/> <section begin=Angular_Momentum/>

Angular_Momentum

Center of mass (rolling without slip) $d_{CM}=r\theta ,$ $v_{CM}=r\omega ,$$a_{MC}=R\alpha =\frac{mg\sin \theta /}{m+(I_{cm}/r^2)}$

▭ Total angular momentum and net torque: $d\overrightarrow{L}/dt=\sum \overrightarrow{\tau }$ $={\overrightarrow{l}}_1+{\overrightarrow{l}}_2+...;$ $\overrightarrow{l}=\overrightarrow{r}\times \overrightarrow{p}$ for a single particle. $L_{total}=I\omega .$

▭ Precession of a top ${\omega }_P=mrg/(I\omega ).$ <section end=Angular_Momentum/> <section begin=Static_Equilibrium_and_Elasticity/>

Static_Equilibrium_and_Elasticity

Equilibrium $\sum {\overrightarrow{F}}_j=0=\sum {\overrightarrow{\tau }}_j.$ Stress = elastic modulus · strain (analogous to Force = k · Δ x )

▭ (Young's , Bulk , Shear) modulus: $(\frac{F_{\perp }}{A}=Y\cdot \frac{\mathrm{\Delta }L}{L_0},\mathrm{\Delta }p=B\cdot \frac{-\mathrm{\Delta }V}{V_0},\frac{F_{\parallel }}{A}=S\cdot \frac{\mathrm{\Delta }x}{L_0})$ <section end=Static_Equilibrium_and_Elasticity/> <section begin=Gravitation/>

Gravitation

Newton's law of gravity ${\overrightarrow{F}}_{12}=G\frac{m_1{m}_2}{r^2}{\hat{r}}_{12}$

▭ Earth's gravity $g=G\frac{M_E}{r^2}$

▭ Gravitational PE beyond Earth $U=-G\frac{M_{E}m}{r}$

▭ Energy conservation $\frac{1}{2}m{v}_1^2-G\frac{Mm}{r_1}=\frac{1}{2}m{v}_2^2-G\frac{Mm}{r_2}$

▭ Escape velocity $v_{esc}=\sqrt{\frac{2G{M}_E}{r}}$

▭ Orbital speed $v_{orbit}=\sqrt{\frac{G{M}_E}{r}}$

▭ Orbital period $T=2\pi \sqrt{\frac{r^3}{G{M}_E}}$

▭ Energy in circular orbit $E=K+U=-\frac{Gm{M}_E}{2r}$

▭ Conic section $\frac{\alpha }{r}=1+e\cos \theta$

▭ Kepler's third law $T^2=\frac{4{\pi }^2}{GM}{a}^3$

▭ Schwarzschild radius $R_S=\frac{2GM}{c^2}$ <section end=Gravitation/> <section begin=Fluid_Mechanics/>

Fluid_Mechanics

Mass density $\rho =m/V$ ▭ Pressure $P=F/A$

Pressure is the weight per unit area of the fluid above a point.

• Template:Green

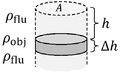
Template:Spaces▭ $B={\rho }_{flu}(A\mathrm{\Delta }h)g$ and ▭ $W={\rho }_{obj}(A\mathrm{\Delta }h)g=M_{obj}g$

▭ Pressure vs depth/height (constant density)$p=p_o+\rho gh\Leftarrow dp/dy=-\rho g$

▭ Absolute vs gauge pressure $p_{abs}=p_g+p_{atm}$

▭ Pascal's principle: $F/A$ depends only on depth, not on orientation of A.

▭ Volume flow rate $Q=dV/dt$

▭ Continuity equation ${\rho }_1{A}_1{v}_1={\rho }_2{A}_2{v}_2$$\Rightarrow A_1{v}_1=A_2{v}_2\text{ if }\rho =const.$

▭ Bernoulli's principle $p_1+\frac{1}{2}\rho v_1^2+\rho g{y}_1=p_2+\frac{1}{2}\rho v_2^2+\rho g{y}_2$

▭ Viscosity $\eta =\frac{FL}{vA}$ where F is the force applied by a fluid that is moving along a distance L from an area A.

▭ Poiseuille equation $p_2-p_1=QR$ where $R=\frac{8\eta \ell }{\pi r^4}$ is "resistance" for a pipe of radius $r$ and length $\ell$.

<section end=Fluid_Mechanics/> <section begin=Oscillations/>

Oscillations

Frequency $f$, period $T$ and angular frequency $\omega :$ $fT=1,\omega T=2\pi$

▭ Simple harmonic motion $x(t)=A\cos (\omega t+\varphi ),$ $v(t)=-A\omega \sin (\omega t+\varphi ),$ $a(t)=-A{\omega }^2\cos (\omega t+\varphi )$ also models the x-component of uniform circular motion.

▭ For $(A,\omega )$ positive: $x_{max}=A,v_{max}=A\omega ,a_{max}=A{\omega }^2$

▭ Mass-spring $\omega =2\pi /T=2\pi f=\sqrt{k/m};$

▭ Energy $E_{Tot}=\frac{1}{2}k{x}^2+\frac{1}{2}m{v}^2=\frac{1}{2}m{v}_{max}^2=\frac{1}{2}k{x}_{max}^2\Rightarrow$$v=\pm \sqrt{\frac{k}{m}(A^2-x^2)}$

▭ Simple pendulum $\omega \approx \sqrt{g/L}$

▭ Physical pendulum $\tau =-MgL\sin \theta \approx -MgL\theta \Rightarrow$$\omega =\sqrt{mgL/I}$ and $L$ measures from pivot to CM.

▭ Torsional pendulum $\tau =-\kappa \theta$$\Rightarrow \omega =\sqrt{I/\kappa }$

▭ Damped harmonic oscillator $m\frac{d^{2}x}{d{t}^2}=-kx-b\frac{dx}{dt}$$\Rightarrow x=A_0{e}^{\frac{b}{2m}t}\cos (\omega t+\varphi )$ where $\omega =\sqrt{{\omega }_0^2-{\left(\frac{b}{2m}\right)}^2}$ and ${\omega }_0=\sqrt{\frac{k}{m}}.$

▭ Forced harmonic oscillator (MIT wiki!) $m\frac{d^{2}x}{d{t}^2}=-kx-b\frac{dx}{dt}+F_0\sin \omega t$$\Rightarrow x=A{e}^{\frac{b}{2m}t}\cos (\omega t+\varphi )$ where $A=\frac{F_0}{\sqrt{m^2(\omega -{\omega }_0{)}^2+b^2{\omega }^2}}$. <section end=Oscillations/> <section begin=Waves/>

Waves

Wave speed (phase velocity) $v=\lambda /T=\lambda f=\omega /k$ where $k=2\pi /\lambda$ is wavenumber.

▭ Wave and pulse speed of a stretched string $=\sqrt{F_T/\mu }$ where $F_T$ is tension and $\mu$ is linear mass density.

▭ Speed of a compression wave in a fluid $v=\sqrt{B/\rho }.$

▭ Periodic travelling wave $y(x,t)=A\sin (kx\mp \omega t)$ travels in the positive/negative direction. The phase is $kx\mp \omega t$ and the amplitude is $A$.

▭ The resultant of two waves with identical amplitude and frequency $y_R(x,t)=[2A\cos \left(\frac{\varphi }{2}\right)]\sin (kx-\omega t+\frac{\varphi }{2})$ where $\varphi$ is the phase shift.

▭ This wave equation ${\partial }^{2}y/\partial t^2=v_w^2{\partial }^{2}y/\partial x^2$ is linear in $y=y(x,t)$

▭ Power in a tranverse stretched string wave $P_{ave}=\frac{1}{2}\mu A^2{\omega }^{2}v$.

▭ Intensity of a plane wave $I=P/A\Rightarrow \frac{P}{4\pi r^2}$ in a spherical wave.

▭ Standing wave $y(x,t)=A\sin (kx)\cos (\omega t+\varphi )$ For symmetric boundary conditions ${\lambda }_n=2\pi /k_n=\frac{2}{\pi }L$ $n=1,2,3,...$, or equivalently $f=n{f}_1$ where $f_1=\frac{v}{2L}$ is the fundamental frequency. <section end=Waves/> <section begin=Sound/>

Sound

Pressure and displacement fluctuations in a sound wave $P=\mathrm{\Delta }{P}_{max}\sin (kx\mp \omega t+\varphi )$ and $s=s_{max}\cos (kx\mp \omega t+\varphi )$

▭ Speed of sound in a fluid $v=f\lambda =\sqrt{\beta /\rho }$, ▭ in a solid $\sqrt{Y/\rho }$, ▭ in an idal gas $\sqrt{\gamma RT/M}$, ▭ in air $331\frac{m}{s}\sqrt{\frac{T_K}{273K}}=331\frac{m}{s}\sqrt{1+\frac{T_C}{273^{o}C}}$

▭ Decreasing intensity spherical wave $I_2=I_1{\left(\frac{r_1}{r_2}\right)}^2$

▭ Sound intensity $I=\frac{⟨P⟩}{A}=\frac{{\left(\mathrm{\Delta }{P}_{max}\right)}^2}{2\rho v}$ ▭  ...level $10{\log }_{10}I/I_0$

▭ Resonance tube One end closed: ${\lambda }_n=\frac{4}{n}L,$ $f_n=n\frac{v}{4L},$ $n=1,3,5,...$ ▭ Both ends open: ${\lambda }_n=\frac{2}{n}L,$ $f_n=n\frac{v}{2L},$ $n=1,2,3,...$

▭ Beat frequency $f_{beat}=|f_2-f_1|$

▭ (nonrelativistic) Doppler effect $f_o=f_s\frac{v\pm v_o}{v\mp v_s}$ where $v$ is the speed of sound, $v_s$ is the velocity of the source, and $v_o$ is the velocity of the observer.

▭ Angle of shock wave $\sin \theta =v/v_s=1/M$ where $v$ is the speed of sound, $v_s$ is the speed of the source, and $M$ is the Mach number. <section end=Sound/>