OpenStax University Physics/V2

http://cnx.org/content/col12074/latest/

Temperature and Heat

$T_C=\frac{5}{9}(T_F-32)$ relates Celsius to Fahrenheit temperature scales. $T_K=T_C+273.15$ relates Kelvin to Celsius.

▭ Linear thermal expansion: $\mathrm{\Delta }L=\alpha L\mathrm{\Delta }T$ relates a small change in length to the total length $L$, where $\alpha$ is the coefficient of linear expansion.
▭ For expansion in two and three dimensions: $\mathrm{\Delta }A=2\alpha A\mathrm{\Delta }T$ and $\mathrm{\Delta }V=\beta V\mathrm{\Delta }T$, respectively.
▭ Heat transfer is $Q=mc\mathrm{\Delta }T$ where $c$ is the specific heat capacity. In a calorimeter, $Q_{cold}+Q_{hot}=0$
▭ Latent heat due to a phase change is $Q=m{L}_f$ for melting/freezing and $Q=m{L}_v$ for evaporation/condensation.
▭ Heat conduction (power): $P=\frac{kA(T_h-T_c)}{d}$ where $k$ is heat conductivity and $d$ is thickness and $A$ is area.
▭ $P_{net}=\sigma eA(T_2^4-T_1^4)$ is the radiative energy transfer rate where $e$ is emissivity and $\sigma$ is the Stefan–Boltzmann constant.

The Kinetic Theory of Gases

Ideal gas law: Pressure×Volume $=pV=nRT=N{k}_{B}T$ where $n$ is the number of moles and $T$ is an absolute temperature.

▭ $N=n{N}_A$ is the number of particles. Gas constant $R$ = 8.3 J K⁻¹/mol
▭ Avegadro's number: $N_A$ = 6.02×10²³. Boltzmann's constant: $k_B$ = 1.38×10⁻²³J/K.
▭ Van der Waals equation $[p+a(nV{)}^2](V-nb)=nRT$
▭ RMS speed $v_{rms}=\sqrt{\overline{v^2}}=\sqrt{\frac{3RT}{M}}=\sqrt{\frac{3k_{B}T}{m}}$ where the overline denotes mean, $m$ is a particle's mass and $M$ is the molar mass.
▭ Mean free path $\lambda =\frac{V}{4\sqrt{2}\pi r^{2}N}=\frac{k_{B}T}{4\sqrt{2}\pi r^{2}p}=v_{rms}\tau$ where $\tau$ is the mean-free-time
▭ Internal energy of an ideal monatomic gas $E_{int}=\frac{3}{2}N{k}_{B}T=N\bar{K}$, where $\bar{K}=$ average kinetic energy of a particle.
▭ $Q=n{C}_V\mathrm{\Delta }T$ defines the molar heat capacity at constant volume.
▭ $C_V=\frac{d}{2}R$ for ideal gas with $d$ degrees of freedom
▭ Maxwell–Boltzmann speed distribution $f(v)=\frac{4}{\sqrt{\pi }}{\left(\frac{m}{2k_{B}T}\right)}^{3/2}{v}^2{e}^{-m{v}^2/2k_{B}T}$
▭ Average speed $\overline{v}=\sqrt{\frac{8}{\pi }\frac{RT}{M}}$ ▭ Peak velocity $v_p=\sqrt{\frac{2RT}{M}}$

The First Law of Thermodynamics

(Pressure, volume, temperature) remain constant in an (isobaric, isochoric, isothermal) process. Heat is not transferred in an adiabatic process.

▭ Equation of state $f(p,V,T)=0$ ▭ Work done by a system $W=\underset{V_1}{\overset{V_2}{\int }}pdV$
▭ Internal energy $E_{int}=\sum _i({\bar{K}}_i+{\bar{U}}_i)$ is a sum over all particles of kinetic and potential energies
▭ First law $\mathrm{\Delta }{E}_{int}=Q-W$ (Q is heat going in and W is work done by as shown in the figure)
▭ $C_p=C_V+R$ is the molar heat capacity at constant volume
▭ $p{V}^{\gamma }=\text{constant}$ for an adiabatic process in an ideal gas, where the heat capacity ratio $\gamma =C_p/C_V$

The Second Law of Thermodynamics

$W=Q_h-Q_c=$ work done in a heat engine cycle. ▭ Efficiency $=e=\frac{W}{Q_h}=1-\frac{Q_c}{Q_h}$

▭ Coefficient of performance for a refrigerator $K_R=\frac{Q_c}{W}=\frac{Q_c}{Q_h-Q_c}$, and heat pump $K_P=\frac{Q_h}{W}=\frac{Q_h}{Q_h-Q_c}$
▭ Entropy change $\mathrm{\Delta }S=\frac{Q}{T}$ (reversible process at constant temperature) $\to \underset{A}{\overset{B}{\int }}\frac{dQ}{T}=S_B-S_A$
▭ $\oint \frac{dQ}{T}$ for any cyclic process $\to \underset{A}{\overset{B}{\int }}\frac{dQ}{T}=S_B-S_A$ is path independent.
▭ $\mathrm{\Delta }S\ge 0$ for any closed system. $\underset{T\to 0}{\lim }\mathrm{\Delta }S=0$ for any isothermal process.

<section begin=5 />

Electric Charges and Fields

Coulomb's Law $\overrightarrow{F}=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r_{12}^2}{\hat{r}}_{12}$ where the vacuum permittivity ${\epsilon }_0=$ 8.85×10⁻¹² F/m.

Elementary charge = e = 1.602×10⁻¹⁹C (electrons have charge q=−e and protons have charge q=+e.)

Dipole moment

▭ By superposition, $\overrightarrow{F}=\frac{1}{4\pi {\epsilon }_0}Q\sum _{i=1}^N\frac{q_i}{r_{Qi}^2}{\hat{r}}_{Qi}$ where ${\overrightarrow{r}}_{Qi}={\overrightarrow{r}}_Q-{\overrightarrow{r}}_i$
▭ Electric field $\overrightarrow{F}=Q\overrightarrow{E}$ where $\overrightarrow{E}({\overrightarrow{r}}_P)=\frac{1}{4\pi {\epsilon }_0}\sum _{i=1}^N\frac{q_i}{r_{Pi}^2}{\hat{r}}_{Pi}$ is the field at ${\overrightarrow{r}}_P$ due to charges at ${\overrightarrow{r}}_i$
▭ The field above an infinite wire $\overrightarrow{E}(z)=\frac{1}{4\pi {\epsilon }_0}\frac{2\lambda }{z}\hat{k}$ and above an infinite plane $\overrightarrow{E}=\frac{\sigma }{2{\epsilon }_0}\hat{k}$
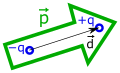
▭ An electric dipole $\overrightarrow{p}=q\overrightarrow{d}$ in a uniform electric field experiences the torque $\tau =\overrightarrow{p}\times \overrightarrow{E}$

<section end=5 /><section begin=6 />

Gauss's Law

 closed .. open

Flux for a uniform electric field $\mathrm{\Phi }=\overrightarrow{E}\cdot \overrightarrow{A}$ $\to \mathrm{\Phi }=\int \overrightarrow{E}\cdot d\overrightarrow{A}=\int \overrightarrow{E}\cdot \hat{n}dA$ in general.

<section begin=6 />

▭ Closed surface integral $\mathrm{\Phi }=\oint \overrightarrow{E}\cdot d\overrightarrow{A}=\oint \overrightarrow{E}\cdot \hat{n}dA$
▭ Gauss's Law $=q_{enc}={\epsilon }_0\oint \overrightarrow{E}\cdot d\overrightarrow{A}$. In simple cases: $E\int dA=E{A}^{*}=\frac{q_{enc}}{{\epsilon }_0}$
▭ Electric field just outside the surface of a conductor $\overrightarrow{E}=\frac{\sigma }{{\epsilon }_0}$

<section end=6 /><section begin=7 />

Electric Potential

Electric potential $\mathrm{\Delta }{V}_{AB}=V_A-V_B=-\underset{A}{\overset{B}{\int }}\overrightarrow{E}\cdot d\overrightarrow{\ell }$. Change in potential energy $=q\mathrm{\Delta }V=\mathrm{\Delta }U$

▭  Electron (proton) mass = 9.11×10⁻³¹kg (1.67× 10⁻²⁷kg). Electron volt: 1 eV = 1.602×10⁻¹⁹J
▭  Near an isolated point charge $V(r)=k\frac{q}{r}$ where $k=\frac{1}{4\pi {\epsilon }_0}$ =8.99×10⁹ N·m/C² is the Coulomb constant.
▭ Work done to assemble N particles $W_{12...N}=\sum _{i=1}^N\sum _{j=1}^{i-1}\frac{q_i{q}_j}{r_{ij}}=\frac{k}{2}\sum _{i=1}^N\sum _{j=1}^N\frac{q_i{q}_j}{r_{ij}}\text{ for }i\ne j$
▭ Electric potential due to N charges. $V_P=k\sum _1^N\frac{q_i}{r_i}$. For continuous charge $V_P=k\int \frac{dq}{r}$. For a dipole, $V=k\frac{\overrightarrow{p}\cdot \overrightarrow{\hat{r}}}{r^2}$.
▭ Electric field as gradient of potential $\overrightarrow{E}=-\frac{\partial V}{\partial x}\hat{i}-\frac{\partial V}{\partial y}\hat{j}-\frac{\partial V}{\partial z}\hat{k}=-\overrightarrow{\mathrm{\nabla }}V$ ▭ Del operator^note: Template:Nowrap beginCartesian $\overrightarrow{\mathrm{\nabla }}=\hat{i}\frac{\partial }{\partial x}+\hat{j}\frac{\partial }{\partial y}+\hat{k}\frac{\partial }{\partial z}\text{; }$Template:Nowrap endCylindrical $\overrightarrow{\mathrm{\nabla }}=\hat{r}\frac{\partial }{\partial r}+\hat{\varphi }\frac{\partial }{\partial \varphi }+\hat{z}\frac{\partial }{\partial z}\text{; }$Spherical $\overrightarrow{\mathrm{\nabla }}=\hat{r}\frac{\partial }{\partial r}+\hat{\theta }\frac{\partial }{\partial \theta }+\hat{\varphi }\frac{\partial }{\partial \varphi }\text{.}$

<section end=7 /><section begin=8 />

Capacitance

$Q=CV$ defines capacitance. For a parallel plate capacitor, $C={\epsilon }_0\frac{A}{d}$ where A is area and d is gap length.

▭ $4\pi {\epsilon }_0\frac{R_1{R}_2}{R_2-R_1}$ and $\frac{2\pi {\epsilon }_0\ell }{\ln (R_2/R_1)}$ for a spherical and cylindrical capacitor, respectively
▭ For capacitors in series (parallel) $\frac{1}{C_S}=\sum \frac{1}{C_i}(C_P=\sum C_i)$
▭  $u=\frac{1}{2}QV=\frac{1}{2}C{V}^2=\frac{1}{2C}{Q}^2$ ▭ Stored energy density $u_E=\frac{1}{2}{\epsilon }_0{E}^2$
▭ A dielectric with $\kappa >1$ will decrease the capacitor's electric field $E=\frac{1}{\kappa }{E}_0$ and stored energy $U=\frac{1}{\kappa }{U}_0$, but increase the capacitance $C=\kappa C_0$ due to the induced electric field ${\overrightarrow{E}}_i=(\frac{1}{\kappa }-1){\overrightarrow{E}}_0$

<section end=8 /><section begin=9 />

Current and Resistance

Current (1A=1C/s) $I=dQ/dt=nq{v}_{d}A$ where $(n,q,v_d)=$ (density, charge, drift velocity) of the carriers.

▭ $I=JA\to \int \overrightarrow{J}\cdot d\overrightarrow{A}$ , $A$ is the perpendicular area, and $J$ is current density. $\overrightarrow{E}=\rho \overrightarrow{J}$ is electric field, where $\rho$ is resistivity.
▭ Resistivity varies with temperature as $\rho ={\rho }_0[1+\alpha (T-T_0)]$. Similarily, $R=R_0[1+\alpha \mathrm{\Delta }T]$ where $R=\rho \frac{L}{A}$ is resistance (Ω)
▭ Ohm's law $V=IR$ ▭  Power $=P=IV=I^{2}R=V^2/R$

<section end=9 /><section begin=10 />

Direct-Current Circuits

Terminal voltage $V_{terminal}=\epsilon -I{r}_{eq}$ where $r_{eq}$ is the internal resistance and $\epsilon$ is the electromotive force.
▭ Resistors in series and parallel: $R_{series}=\sum _{i=1}^N{R}_i$ ▭ $R_{parallel}^{-1}=\sum _{i=1}^N{R}_i^{-1}$
▭ Kirchoff's rules. Loop:$\sum I_{in}=\sum I_{out}$ Junction: $\sum V=0$

▭ $V_{terminal}^{series}=\sum _{i=1}^N{\epsilon }_i-I\sum _{i=1}^N{r}_i$ ▭ $V_{terminal}^{parallel}=\epsilon -I\sum _{i=1}^N{\left(\frac{1}{r_i}\right)}^{-1}$ where $r_i$ is internal resistance of each voltage source.
▭ Charging an RC (resistor-capacitor) circuit: $q(t)=Q(1-e^{-t/\tau })$ and $I=I_0{e}^{-t/\tau }$ where $\tau =RC$ is RC time, $Q=\epsilon C$ and $I_0=\epsilon /R$.
▭ Discharging an RC circuit: $q(t)=Q{e}^{-t/\tau }$ and $I(t)=-\frac{Q}{RC}{e}^{-t/\tau }$

<section end=10 /><section begin=11 />

Magnetic Forces and Fields

• 
  Cross product $|\overrightarrow{a}\times \overrightarrow{b}|$$=ab\sin \theta$
• 
  Hall effect ${\overrightarrow{v}}_d=\overrightarrow{E}\times \overrightarrow{B}/B^2$
• 
  Mass spectrometer in special case that both magnetic fields are equal

▭ $\overrightarrow{F}=q\overrightarrow{v}\times \overrightarrow{B}$ is the force due to a magnetic field on a moving charge.
▭ For a current element oriented along $\overrightarrow{d\ell },d\overrightarrow{F}=I\overrightarrow{d\ell }\times \overrightarrow{B}$.

▭ The SI unit for magnetic field is the Tesla: 1T=10⁴ Gauss.
▭ Gyroradius $r=\frac{mB}{qB}.$ Period $T=\frac{2\pi m}{qB}.$
▭ Torque on current loop $\overrightarrow{\tau }=\overrightarrow{\mu }\times \overrightarrow{B}$ where $\overrightarrow{\mu }=NIA\hat{n}$ is the dipole moment. Stored energy $U=\overrightarrow{\mu }\cdot \overrightarrow{B}.$
▭ Drift velocity in crossed electric and magnetic fields $v_d=\frac{E}{B}$
▭ Hall voltage = $V$ where the electric field is $E=V/\ell =B{v}_d=\frac{IB}{neA}$
▭ Charge-to-mass ratio $q/m=\frac{E}{B{B}_{0}r}$ where the $E$ and $B$ fields are crossed and $E=0$ when the magnetic field is $B_0$

<section end=11 /><section begin=12 />

Sources of Magnetic Fields

▭ Permeability of free space ${\mu }_0=4\pi \times 10^{-7}$ T·m/A
▭ Force between parallel wires $\frac{F}{\ell }=\frac{{\mu }_0{I}_1{I}_2}{2\pi r}$
▭ Biot–Savart law $\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\underset{wire}{\int }\frac{Id\overrightarrow{\ell }\times \hat{r}}{r^2}$Template:Clear
▭ Ampère's Law:$\oint \overrightarrow{B}\cdot d\overrightarrow{\ell }={\mu }_0{I}_{enc}$
▭ Magnetic field due to long straight wire $B=\frac{{\mu }_{0}I}{2\pi R}$ ▭ At center of loop $B=\frac{{\mu }_{0}I}{2R}$
▭ Inside a long thin solenoid $B={\mu }_{0}nI$ where $n=N/\ell$ is the ratio of the number of turns to the solenoid's length.
▭ Inside a toroid $B=\frac{{\mu }_{0}N}{2\pi r}$

▭ The magnetic field inside a solenoid filled with paramagnetic material is $B=\mu nI$ where $\mu =(1+\chi ){\mu }_0$ is the permeability

<section end=12 /><section begin=13 />

Electromagnetic Induction

Magnetic flux ${\mathrm{\Phi }}_m=\underset{S}{\int }\overrightarrow{B}\cdot \hat{n}dA$ ▭ Electromotive force $\epsilon =-N\frac{d{\mathrm{\Phi }}_m}{dt,}$ (Faraday's law)
▭ Motional emf $\epsilon =B\ell v,$ ▭ rotating coil $NBA\omega \sin \omega t$
▭ Motional emf around circuit $\epsilon =\oint \overrightarrow{E}\cdot d\overrightarrow{\ell }=-\frac{d{\mathrm{\Phi }}_m}{dt}$

<section end=13 /><section begin=14 />

Inductance

The SI unit for inductance is the Henry: 1H=1V·s/A ▭ Mutual inductance: $M\frac{d{I}_2}{dt}=N_1\frac{d{\mathrm{\Phi }}_{12}}{dt}=-{\epsilon }_1$ where ${\mathrm{\Phi }}_{12}$ is the flux through 1 due to the current in 2 and ${\epsilon }_1$ is the emf in 1. Likewise, it can be shown^SEE TALK that, $M\frac{d{I}_1}{dt}=-{\epsilon }_2$.

▭ Self-inductance $N{\mathrm{\Phi }}_m=LI\to \epsilon =-L\frac{dI}{dt}$ ▭  $L_{\text{solenoid}}\approx {\mu }_0{N}^{2}A\ell ,$$L_{\text{toroid}}\approx \frac{{\mu }_0{N}^{2}h}{2\pi }\ln \frac{R_2}{R_1}.$ Stored energy $U=\frac{1}{2}L{I}^2.$ ▭ $I(t)=\frac{\epsilon }{R}(1-e^{-t/\tau })$is the current in an LR circuit where $\tau =L/R$ is the LR decay time.
▭ The capacitor's charge on an LC circuit $q=q_0\cos (\omega t+\varphi )$ where $\omega =\sqrt{\frac{1}{LC}}$ is angular frequency
▭ LRC circuit $q(t)=q_0{e}^{-Rt/2L}\cos ({\omega }^{\prime }t+\varphi )$ where ${\omega }^{\prime }=\sqrt{\frac{1}{LC}+{\left(\frac{R}{2L}\right)}^2}$

<section end=14 /><section begin=15 />

Alternating-Current Circuits

RLC circiut

AC voltage and current $v=V_0\sin (\omega t-\varphi )$ if $i=I_0\sin \omega t.$
▭ RMS values $I_{rms}=\frac{I_0}{\sqrt{2}}$ and $V_{rms}=\frac{V_0}{\sqrt{2}}$ ▭ Impedance $V_0=I_{0}X$

▭ Resistor $V_0=I_0{X}_R,\varphi =0,$ where $X_R=R$
▭ Capacitor $V_0=I_0{X}_C,\varphi =-\frac{\pi }{2},$ where $X_C=\frac{1}{\omega C}$ ▭ Inductor $V_0=I_0{X}_L,\varphi =+\frac{\pi }{2},$ where $X_L=\omega L$
▭ RLC series circuit $V_0=I_{0}Z$ where $Z=\sqrt{R^2+{(X_L-X_C)}^2}$ and $\varphi ={\tan }^{-1}\frac{X_L-X_C}{R}$
▭ Resonant angular frequency ${\omega }_0=\sqrt{\frac{1}{LC}}$ ▭ Quality factor $Q=\frac{{\omega }_0}{\mathrm{\Delta }\omega }=\frac{{\omega }_{0}L}{R}$
▭ Average power $P_{ave}=\frac{1}{2}{I}_0{V}_0\cos \varphi =I_{rms}{V}_{rms}\cos \varphi$, where $\varphi =0$ for a resistor.
▭ Transformer voltages and currents $\frac{V_S}{V_P}=\frac{N_S}{N_P}=\frac{I_P}{I_S}$

<section end=15 /><section begin=16 />

Electromagnetic Waves

Displacement current $I_d={\epsilon }_0\frac{d{\mathrm{\Phi }}_E}{dt}$ where ${\mathrm{\Phi }}_E=\int \overrightarrow{E}\cdot d\overrightarrow{A}$ is the electric flux.

Maxwell's equations $\begin{array}{cccc}{\oint }_S\overrightarrow{E}\cdot \mathrm{d}\overrightarrow{A}& =\frac{1}{{ϵ}_0}{Q}_{in}& {\oint }_S\overrightarrow{B}\cdot \mathrm{d}\overrightarrow{A}& =0\\ {\oint }_C\overrightarrow{E}\cdot \mathrm{d}\overrightarrow{\ell }& =-\underset{S}{\int }\frac{\partial \overrightarrow{B}}{\partial t}\cdot \mathrm{d}\overrightarrow{A}& {\oint }_C\overrightarrow{B}\cdot \mathrm{d}\overrightarrow{\ell }& ={\mu }_{0}I+{ϵ}_0{\mu }_0\frac{\mathrm{d}{\mathrm{\Phi }}_E}{\mathrm{d}t}\end{array}$
See also http://ethw.org/w/index.php?title=Maxwell%27s_Equations&oldid=157445
▭ Plane EM wave equation $\frac{{\partial }^2{E}_y}{\partial x^2}={\epsilon }_0{\mu }_0\frac{{\partial }^2{E}_y}{\partial t^2}$ where $c=\frac{1}{\sqrt{{\epsilon }_0\mu }}$ is the speed of light
▭ The ratio of peak electric to magnetic field is $\frac{E_0}{B_0}=c$ and the Poynting vector $\overrightarrow{S}=\frac{1}{{\mu }_0}\overrightarrow{E}\times \overrightarrow{B}$ represents the energy flux
▭ Average intensity $I=S_{ave}=\frac{c{\epsilon }_0}{2}{E}_0^2=\frac{c}{2{\mu }_0}{B}_0^2=\frac{1}{2{\mu }_0}{E}_0{B}_0$
▭ Radiation pressure $p=I/c$ (perfect absorber) and $p=2I/c$ (perfect reflector). <section end=16 />