Physics/A/String vibration/Nonlinear
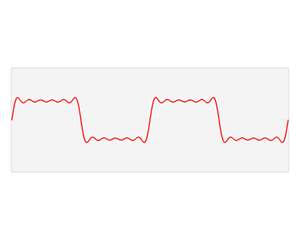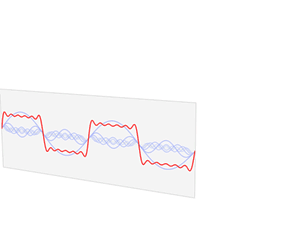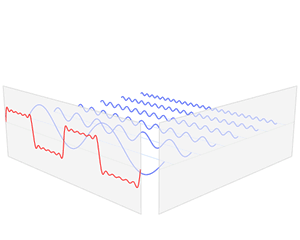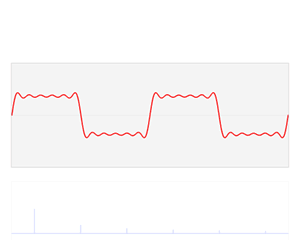

Define
, and .
Transverse standing wave:
Define
Second order differential equation with one variable: https://openstax.org/books/calculus-volume-3/pages/7-2-nonhomogeneous-linear-equations
where is the solution to the homogeneous equation, i.e., solution to
Link to wikipedia:Fourier series?
- https://www.mathsisfun.com/calculus/fourier-series.html
- https://mathworld.wolfram.com/FourierSeries.html
Employ two identities:
and
To find a particular solution, to (?) we first consider two different inhomogeneous equations:
NOW
Recall =>
If is proportional to , then , and: =>
If is proportional to , then and: = => =>. Now use .
By the linearity of the operator we see that a particular solution to (?) is the sum of
In these units the speed of a wave is . This permits us to write an expression that does not depend on the choice of units.[1] Relating the wavenumber of the lowest order mode to string length by :
<math></math>
Other identities
wikipedia:special:permalink/1017302768
Template:Spaces*Template:Spaces Template:Spaces*Template:Spaces Template:Spaces*Template:Spaces Template:Spaces*Template:Spaces Template:Spaces*Template:Spaces Template:Spaces*Template:Spaces Template:Spaces*Template:Spaces Template:Spaces*Template:Spaces
After modifying an equation from Wikipedia:
- ↑ See David R Rowland 2011 Eur. J. Phys. 32 1475, equation 11