Template:PhyseqM

Please do not use this template. Instead go to Physics equations/Equations or a subpage and transclude from there.

Sample Superstructure

Sample Substructure

SampleName

• Foo

<section end=SampleName/> Call with {{PhyseqM|transcludesection=SampleName}}

SampleSubname

used for alternative versions of the same equation

Geometry and algebra

CircleSphere

• $C_{\odot }=2\pi r$ is the circumference of circle;  $A_{\odot }=\pi r^2$ is its area.
• $A_{◯}=4\pi r^2$ is the surface area of a sphere;   $V_{◯}=\frac{4}{3}\pi r^3$ is its volume.

<section end=CircleSphere/> Call with {{PhyseqM|transcludesection=CircleSphere}}

SimpleDefinitionThetaRadians

• $\theta =\frac{s}{r}$ defines angle (in radians), where s is arclength and r is radius.

<section end=SimpleDefinitionThetaRadians/> Call with {{PhyseqM|transcludesection=SimpleDefinitionThetaRadians}}

TrigWithoutVectors

• $\sin A=\frac{\text{opposite}}{\text{hypotenuse}}=\frac{a}{c}.$ (where A is the angle shown)
• $\cos A=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{b}{c}.$
• $\tan A=\frac{\text{opposite}}{\text{adjacent}}=\frac{a}{b}=\frac{\sin A}{\cos A}.$

<section end=TrigWithoutVectors/> Call with {{PhyseqM|transcludesection=TrigWithoutVectors}}

InverseTrigFunctions

• $\sin ({\sin }^{-1}(z))=z$ and $si{n}^{-1}(\sin \theta )=\theta$ defines the arcsine function as the inverse of the sine. Similarly, ${\tan }^{-1}$ is called the arctangent, or the inverse tangent, and ${\cos }^{-1}$ is called arccosine, or the inverse cosine and so forth. In general, $f(f^{-1}(y))=y$ and $f^{-1}((f(x))=x$ for any function and its inverse. Complexities occur whenever the inverse is not a true function; for example, since $\tan (\theta )=\tan (\theta +\pi )$, the inverse is multi-valued: ${\tan }^{-1}(\tan \theta )=\theta or\theta +\pi .$

<section end=InverseTrigFunctions/> Call with {{PhyseqM|transcludesection=InverseTrigFunctions}}

First year calculus

CalculusBasic

• $\mathrm{\Delta }f=f(x+\mathrm{\Delta }x)-f(x)$,     and the derivative is $\frac{\mathrm{\Delta }f}{\mathrm{\Delta }x}\to \frac{df}{dx}$ in the limit that $\mathrm{\Delta }x\to 0$
• $\frac{d}{dx}f(g(x))=\frac{df}{dg}\frac{dg}{dx}$ is the chain rule.
• $\frac{d}{dx}A{x}^p=(p-1)A{x}^{p-1}$,      $\frac{d}{dx}\ln x=\frac{1}{x}$,     $\frac{d}{dx}{e}^x=e^x$,     $\frac{d}{dx}\sin x=\cos x$,     $\frac{d}{dx}\cos x=-\sin x$
• $\int \frac{df}{dx}dx=f(x)+c$ expresses the fundamental theorem of calculus.

<section end=CalculusBasic/> Call with {{PhyseqM|transcludesection=CalculusBasic}}

RiemannSum

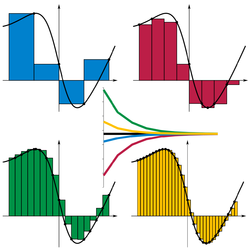
• $\underset{a}{\overset{b}{\int }}f(x)\mathrm{d}x\approx \sum f(x_j)\mathrm{\Delta }{x}_j$ is the Riemann sum representation of the integral of f(x) from x=a to x=b. It is the area under the curve, with contributions from f(x)<0 being negative (if a>b). The sum equals the integral in the limit that the widths of all the intervals vanish (Δx_j→0).

• 
  Left sum
• 
  Right sum
• 
  Middle sum

<section end=RiemannSum/> Call with {{PhyseqM|transcludesection=RiemannSum}}

RiemannSumShort

• $\underset{a}{\overset{b}{\int }}f(x)\mathrm{d}x\approx \sum f(x_j)\mathrm{\Delta }{x}_j$ is the Riemann sum representation of the integral of f(x) from x=a to x=b.

<section end=RiemannSumShort/> Call with {{PhyseqM|transcludesection=RiemannSumShort}}

IntegrateFundamentalTheorem

• The fundamental theorem of calculus allows us to construct integrals from known derivatives:
• $\underset{a}{\overset{b}{\int }}A{x}^n\mathrm{d}x=\{\frac{A}{n+1}{b}^{n+1}-\frac{A}{n+1}{a}^{n+1}\}$
• $\underset{a}{\overset{b}{\int }}A{x}^{-1}\mathrm{d}x=A\ln b-A\ln a=A\ln \frac{b}{a}$

<section end=IntegrateFundamentalTheorem/> Call with {{PhyseqM|transcludesection=IntegrateFundamentalTheorem}}

Vector algebra

VectorComponents

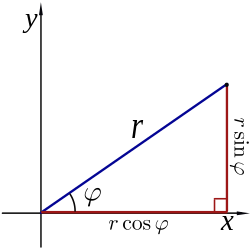
• $x=r\cos \theta$ and $y=r\sin \theta$ are the x and y components of a displacement from the origin to some point. The inverse transformations are:

• $r=\sqrt{x^2+y^2}$, and

• $\theta =\arctan (y/x)$ , which is multi-valued and therefore not a true function.

• $A_x=A\cos \theta$   and   $A_y=A\sin \theta$   are called the x and y components of vector A, respectively.

• $|\overrightarrow{A}|=\sqrt{A_x^2+A_y^2}=A$ is called the magnitude,norm (or sometimes absolute value) of vector A.

• Omission of the arrow indicates that the quantity is the scalar magnitude of that vector. Another notation that distinguishes between a vector and a scalar is boldface font: A is a vector and A= $|$ A $|$ is the scalar magnitude.

<section end=VectorComponents/> Call with {{PhyseqM|transcludesection=VectorComponents}}

VectorAddition

• $\overrightarrow{A}+\overrightarrow{B}=\overrightarrow{C}$ and $\overrightarrow{B}=\overrightarrow{C}-\overrightarrow{A}$ have geometric interpretation as vector addition and subtraction as shown in the figure. Vector addition and subtraction can also be defined through the components. For example, the following two statements are equivalent:
• $\overrightarrow{A}+\overrightarrow{B}=\overrightarrow{C}\iff$ $A_x+B_x=C_x$ AND $A_y+B_y=C_y$

<section end=VectorAddition/> Call with {{PhyseqM|transcludesection=VectorAddition}}

CrossProductVisual

right-hand rule

• $\overrightarrow{A}\times \overrightarrow{B}=\overrightarrow{C}$ is the cross product of $\overrightarrow{A}$ and $\overrightarrow{B}$. The cross product, $\overrightarrow{C}$ is directed perpendicular to $\overrightarrow{A}$ and $\overrightarrow{B}$ by the right hand rule.
• $|\overrightarrow{A}\times \overrightarrow{B}|=C=|AB\sin \theta |$ wehre $\theta$ is the angle between vectors $\overrightarrow{A}$ and $\overrightarrow{B}$.
• $|\overrightarrow{A}\times \overrightarrow{B}|=C$ is also the magnitude of the of the parallelogram defined by the vectors $\overrightarrow{A}$ and $\overrightarrow{B}$.
• $\overrightarrow{A}\times \overrightarrow{B}=0$ if $\overrightarrow{A}$ and $\overrightarrow{B}$ are either parallel or antiparallel.
• The unit vectors obey $\hat{x}\times \hat{y}=\hat{z}$, $\hat{y}\times \hat{z}=\hat{x}$, and $\hat{z}\times \hat{x}=\hat{y}$.

<section end=CrossProductVisual/> Call with {{PhyseqM|transcludesection=CrossProductVisual}}

DotProduct

• $\overrightarrow{A}\cdot \overrightarrow{B}=AB\cos \theta =A_x{B}_x+A_y{B}_y+A_z{B}_z$ is the dot product between two vectors separated in angle by θ.

<section end=DotProduct/> Call with {{PhyseqM|transcludesection=DotProduct}}

CrossProductComponents

$\begin{array}{cccc}\overrightarrow{A}\times \overrightarrow{B}\iff & C_x& =& A_y{B}_z-A_x{B}_y\text{and}\\ & C_y& =& A_z{B}_x-A_x{B}_z\text{and}\\ & C_z& =& A_x{B}_y-A_y{B}_x.\end{array}$ <section end=CrossProductComponents/> Call with {{PhyseqM|transcludesection=CrossProductComponents}}

UnitVectors

• A unit vector is any vector with unit magnitude equal to one. For any nonzero vector, $\hat{V}=\overrightarrow{V}/V$ is a unit vector. An important set of unit vectors is the orthonormal basis associated with Cartesian coordinates:
• $\widehat{𝐢}\cdot \widehat{𝐢}=\widehat{𝐣}\cdot \widehat{𝐣}=\widehat{𝐤}\cdot \widehat{𝐤}=1$
• $\widehat{𝐣}\cdot \widehat{𝐤}=\widehat{𝐤}\cdot \widehat{𝐢}=\widehat{𝐣}\cdot \widehat{𝐤}=0$
• The basis vectors $(\widehat{𝐢},\widehat{𝐣},\widehat{𝐤})$ are also written as $(\hat{x},\hat{y},\hat{z})$, so that any vector may be written $\overrightarrow{A}=A_x\hat{x}+A_y\hat{y}+A_z\hat{z}$. Even more elegance is achieved by labeling the directions with integers: $\overrightarrow{A}=A_1\widehat{e_1}+A_2\widehat{e_2}+A_3\widehat{e_3}$ $=\mathrm{\Sigma }{A}_j\widehat{e_j}.$

<section end=UnitVectors/> Call with {{PhyseqM|transcludesection=UnitVectors}}

Removed templates

PathIntegralOpenClosedSurface

THIS TEMPLATE HAS BEEN REMOVED <section end=PathIntegralOpenClosedSurface/> Call with {{PhyseqM|transcludesection=PathIntegralOpenClosedSurface}}