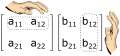Physics/A/Introduction to tensors in physics

This page is currently being used as a sandbox for User:Guy vandegrift/Introduction to tensors in physics

• Preliminary drafts for STRAIN at Physics/A/Introduction to tensors in physics/1

Subpages

---

Error creating thumbnail:

Strain and the gradient of the deformation

Here is the matrix I came up with AFTER talking to BARD

-2	1	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces
1	-2	1	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces
Template:Spaces0Template:Spaces	1	-2	1	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces
Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	1	-2	1	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces
Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	1	-2	1	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces
Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	1	-2	1	Template:Spaces0Template:Spaces
Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	1	-2	1
Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	Template:Spaces0Template:Spaces	1	-2

Recent items on top

---

Most recent on top

Infinite matrix

• Borrowed from https://www.physics.rutgers.edu/~chakhalian/CM2018/HW2_solutions.pdf

This is the identity for sines:

$X=\sin (\theta -\varphi )-2\sin (\theta )+\sin (\theta +\varphi )$

$\sin (\theta -\varphi )=\sin (\theta )\cos (\varphi )-cos(\theta )\sin (\varphi )$

$\sin (\theta +\varphi )=\sin (\theta )\cos (\varphi )+cos(\theta )\sin (\varphi )$

$X=\underset{\sin (\theta )\cos (\varphi )-cos(\theta )\sin (\varphi )}{\underbrace{\sin (\theta -\varphi )}}-2\sin (\theta )+\underset{\sin (\theta )\cos (\varphi )+cos(\theta )\sin (\varphi )}{\underbrace{\sin (\theta +\varphi )}}$

$X=2\sin \theta \cos \varphi -2\sin \theta =(2\cos \varphi -1)\sin \theta$

Eigen values/vectors 2x2 matrix

From Bing: matrix (a, b; b, c)
Eigenvalues: λ1 = (a + c + sqrt((a - c)^2 + 4b^2)) / 2 and λ2 = (a + c - sqrt((a - c)^2 + 4b^2)) / 2
Eigenvectors:  x1 = [b; λ1 - a] and x2 = [b; λ2 - a]

$\left[\begin{array}{cc}a& b\\ b& c\end{array}\right]$

${\lambda }_1=\frac{a+c+\sqrt{(a-c{)}^2+4b^2}}{2}$ Template:Spaces ${\lambda }_1=\frac{a+c-\sqrt{(a-c{)}^2+4b^2}}{2}$

${\overrightarrow{v}}_1=b\hat{x}+({\lambda }_1-a)\hat{y}$Template:Spaces ${\overrightarrow{v}}_2=b\hat{x}+({\lambda }_2-a)\hat{y}$

substitute

$a={\kappa }_x$, $b={\kappa }_S$ to obtain:

$\left[\begin{array}{cc}{\kappa }_x& {\kappa }_S\\ {\kappa }_S& {\kappa }_y\end{array}\right]$

$({\kappa }_x-k)({\kappa }_y-k)-{\kappa }_S^2=0$ this checks

The rest needs to be verified:

$k_1=\frac{{\kappa }_S+{\kappa }_y+\sqrt{({\kappa }_x-{\kappa }_y{)}^2+4{\kappa }_S^2}}{2}$ Template:Spaces $k_2=\frac{{\kappa }_S+{\kappa }_y-\sqrt{({\kappa }_x-{\kappa }_y{)}^2+4{\kappa }_S^2}}{2}$

${\overrightarrow{v}}_1={\kappa }_S\hat{x}+(k_1-{\kappa }_x)\hat{y}$Template:Spaces ${\overrightarrow{v}}_2={\kappa }_S\hat{x}+(k_2-{\kappa }_x)\hat{y}$

check w chatgpt

$k=\frac{{\kappa }_x+{\kappa }_y\pm \sqrt{({\kappa }_x+{\kappa }_y{)}^2-4({\kappa }_x{\kappa }_y-{\kappa }_S^2)}}{2}$Template:Spaces $\overrightarrow{v}={\kappa }_S\hat{x}+(k-{\kappa }_x)\hat{y}$

without subscripts

Template:Multiple image $\left[\begin{array}{cc}\alpha & \gamma \\ \gamma & \beta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=k\left[\begin{array}{c}x\\ y\end{array}\right]$

Two straight lines: $y=\frac{k-\alpha }{\gamma }xy=\frac{\gamma }{k-\beta }x.$

Two linear equations can yield zero, one, or an infinite number of solutions (see image.) In our case, $x=y=0$ is always a solution, but we seek an infinite number of solutions. The next step is so famous it's called "finding the determinant": Set the two slopes equal to each other and solve for $k$

Rotation tensor with dice

The first thing a student should know about tensors is that they organize your knowledge about a system in a very useful way. A vector is known as an entity with magnitude and direction. But it is also a rank-1 tensor. On the two-dimensional plane, it has two components, and for convenience we often take label those components by their projection on two perpendicular unit vectors. If one were to rotate both unit vectors by the angle, θ, then a rotation matrix can be used to predict the new components of a vector. In physics, it is essential that all parameters that describe a system be organized into scalars, vectors and tensors. Here, we restrict our study of the rotation tensor to angles that are integer multiples of 90°.

If $n$ is a integer, ${\underset{\_}{\underset{\_}{R}}}^n$ rotates any vector in the x-y plane by $n\pi /2$ (i.e., multiples of 90°.). Let ${\underset{\_}{\underset{\_}{T}}}^n$ denote matrix multiplication of a tensor by itself $n$ times, with the understanding that  ${\underset{\_}{\underset{\_}{T}}}^0$ equals, $I$, the identity matrix.

1. Find a simple expression for ${\underset{\_}{\underset{\_}{T}}}^4$ (hint: a very simple expression.)
2. Use the vector $[1,1]$ to find ${\underset{\_}{\underset{\_}{T}}}^n$ for $n\in \{1,2,3\}$. You will have to "guess" this value. If you already know the answer, show how a person would guess if they were asked to begin with matrices where all the elements are either Template:Math or Template:Math. Take your effort to "pretend" seriously by working out several such multiplications. If you truly are trying to guess the answer, don't worry if the rotated vector is too large, you can multiply by a factor to ensure that the final vector has the right length.

Ideas

1. Establish by example that the transpose of a orthogonal matrix is its inverse (mention that with complex numbers "orthogonal" becomes "unitary")
2. Show by both example (and perhap a proof) that the rows and columns of an orthogonal matrix are orthogonal unit vectors.

WMF resources on Rotations

Wikipedia resources. It does not seem that Wikipedia has discusses this fact in a way accessible to the non-expert.

• w:Rotation matrix contains an exhaustive list of facts associated with rotations, but the focus is exclusively on how vectors transform.
• w:Tensor#As_multidimensional_arrays also mentions that "the matrix of a linear operator with respect to a basis is a rectangular array $T$ that transforms under a change of basis matrix $R=\left(R_i^j\right)$ by $\hat{T}=R^{-1}TR$."
• w:Change of basis#Endomorphisms obliquely states the rule in a context no beginner would understand, "if Template:Mvar is the square matrix of an endomorphism of Template:Mvar over an "old" basis, and Template:Mvar is a change-of-basis matrix, then the matrix of the endomorphism on the "new" basis is $P^{-1}MP.$" Note: This statement was made in an algebra where ${\underset{\_}{w}}^{\prime }=\underset{\_}{w}\cdot \underset{\_}{\underset{\_}{P}}.$
• Wikibooks has only b:Robotics Kinematics and Dynamics/Description of Position and Orientation

Early version of introduction

• Early introduction draft

1. Story of Raneir Sachs: boredom versus confusion, special relativity, tensor as File:Arrows-eight-long.png.
2. Information counting: Use how much information can be extracted from a collection of equations. For example, what happens when you attempt to solve the following pairs of equations for $x$ and $y$: $(y=x,y=x+1)$ versus $(y=x,y=-x+1)$ versus $(y=x+1,2y=2x+2)$
3. Spring constant as a tensor, Diagonal tensor, Rotations and the eigenvalue problem in a disguised as a few simple algebraic steps. The most extreme example of symmetries occurs when the spring constant tensor is a multiple of the identity matrix: $\overrightarrow{F}=-\tilde{k}\overrightarrow{r}$, where $\tilde{k}=k\tilde{I}$

• The stress and stran tensors are a symmetric tensors, meaning that the stress tensor’s components of each tensor satisfy the equation σ_ij = σ_ji . This symmetry is due to the balance of angular momentum 2. The stress tensor has nine components, but only six of them are independent.

Rotations

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right],$$

$$\left[\begin{array}{c}{F_x}^{\prime }\\ {F_y}^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{F}_x\\ F_x\end{array}\right],$$

In other words, begin with the following six equations:

$$\begin{array}{cccc}{x}^{\prime }& =Cx+Sy& {F_x}^{\prime }& =C{F}_x+S{F_y}^{\prime }\\ y^{\prime }& =-Sx+Cy& {F_y}^{\prime }& =-S{F}_x+C{F_y}^{\prime }\\ F_x& =k_{x}x& F_y& =k_{y}y\\ \end{array}$$

To simplify things, we have defined $C=\cos \theta$ and $S=\sin \theta$. If you are not accustomed to subscripts, make also the following replacements: $f=F_x,$ $g=F_y,$ $k=k_x,$ and $\ell =k_y.$

Use these 6 equations to express ${F_x}^{\prime }$ and ${F_y}^{\prime }$ in terms of $x^{\prime }$ and $y^{\prime }$.

For extra credit, convert your answer in matrix form. For extra extra credit, go to the Wikipedia:Rotation of axes in two dimensions and write a badly needed section on how to transform a 2x2 matrix using the rotation tensor (or you could write a draft by hand or on your favorite word processor,)

Tensor form of Hooke's law

$$dU=\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=\left[\begin{array}{cc}dx& dy\end{array}\right]\left[\begin{array}{cc}{\kappa }_{xx}& {\kappa }_{xy}\\ {\kappa }_{yx}& {\kappa }_{yy}\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

$$dU=\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=\left[\begin{array}{cc}dx& dy\end{array}\right]\left[\begin{array}{cc}{\kappa }_{xx}& {\kappa }_{xy}\\ {\kappa }_{yx}& {\kappa }_{yy}\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

$$\left[\begin{array}{cc}{\kappa }_{xx}& {\kappa }_{xy}\\ {\kappa }_{yx}& {\kappa }_{yy}\end{array}\right]=\left[\begin{array}{cc}{\kappa }_{xx}& {\kappa }_s\\ {\kappa }_s& {\kappa }_{yy}\end{array}\right]+\left[\begin{array}{cc}0& {\kappa }_a\\ -{\kappa }_a& 0\end{array}\right]$$

${\kappa }_s=\frac{{\kappa }_{xy}+{\kappa }_{yx}}{2}$   and   ${\kappa }_a=\frac{{\kappa }_{xy}-{\kappa }_{yx}}{2}$

References

Important

• Linear algebra/Orthogonal matrix---
• w:Infinitesimal strain theory---
• w:Cauchy_stress_tensor---
• w:Deflection (engineering)---
• w:Infinitesimal_strain_theory#Infinitesimal_strain_tensor
• w:Strain_(mechanics)#Strain_tensor
• w:Deformation (physics)
• w:Displacement field (mechanics)
• w:Simple shear and w:Pure shear might be worth mentioning

Unimporant

wikilinks

Wikiversity--- Continuum mechanics/Time derivatives and rates--- Continuum mechanics/Motion and displacement--- Continuum mechanics/Reynolds transport theorem--- Continuum mechanics/Strains and deformations--- Continuum mechanics/Thermodynamics of continua--- Nonlinear finite elements/Kinematics - time derivatives and rates--- Advanced elasticity/Strains and deformations--- Continuum_mechanics/Thermodynamics_of_continua--- [[]]--- [[]]--- [[]]--- [[]]--- [[]]--- Wikibooks--- b:--- b:--- b:--- b:--- b:--- b:--- b:--- b:--- Wikipedia--- w:Eigendecomposition of a matrix w:---

w:Flexural strength--- w:Euler–Bernoulli beam theory--- Elasticity-- w:Alternative stress measures--- -- w:Taylor_series#Taylor_series_in_several_variables--- w:Poisson's ratio--- w:Ellipse#General ellipse--- w:--- w:---

c:Hyperbolic paraboloid structures---

Web

animation spring pendulum--- Figuro free online 3D cad--- You tube video of 2D stress tensor --- Curl contour plot--- User_Interfaces_to_Interact_with_Tensor_Fields--- video on Mohr's circle--- online matrix simulator

Images

• File:Is-plane-plane-s.svg
• File:Secretsharing 3-point.svg
• File:Parallelepiped 2013-11-29.svg
• File:Unstable , neutral, and stable equilibrium.png
• File:Thermohaline Circulation.svg
• File:Tug of war pictogram.svg
• File:Quizbank logo.svg
• 
• File:2D geometric strain.png
• File:Motion3D.png
• Error creating thumbnail:
• 
• File:PassiveActive.JPG
• File:Non-commutative rotation of dice.png
• 
• File:2Tensor representation 2D or 3D.png
• File:Arrows-eight-short.png
• File:General ellipse.png
• Error creating thumbnail:
• 
• File:Asymmetricwave2.png
• 
• Error creating thumbnail:
• Error creating thumbnail:
• 
• File:Parabol-el-zy-hy-s.svg
• 
• 
• 
• 
• Error creating thumbnail: